Пирамида — это трехмерная геометрическая фигура, которая имеет множество интересных свойств. Одним из них является то, что пирамиду можно разрезать плоскостью на две части. Такое разрезание называется сечением пирамиды. Однако нередко возникает вопрос: какая плоская фигура может быть получена в результате такого сечения?
Ответ на этот вопрос зависит от того, как плоскость проходит через пирамиду. Если плоскость проходит через вершину пирамиды и параллельна основанию, то сечение будет иметь форму многоугольника. Этот многоугольник будет полигоном, а число его сторон будет равно числу сторон основания пирамиды.
Если плоскость проходит через вершину пирамиды, но не параллельна основанию, то сечение будет иметь форму многоугольной звезды. Этот многоугольник будет иметь основание, которое является проекцией основания пирамиды на плоскость сечения, а плоскость сечения будет задавать форму вершин многоугольника.
Таким образом, сечение пирамиды может принимать разные формы в зависимости от того, как плоскость проходит через эту трехмерную фигуру. Результатом сечения может быть как простой многоугольник, так и сложная многоугольная звезда. Исследование этих форм может привести к удивительным геометрическим открытиям и новым пониманию трехмерного пространства.
- Что такое пирамида
- Описание понятия «пирамида»
- Главные характеристики пирамиды
- Сечение пирамиды
- Что представляет собой сечение пирамиды
- Какими инструментами можно выполнить сечение пирамиды
- Какую плоскую фигуру можно получить в результате
- Описание возможных фигур
- Примеры плоских фигур, полученных в результате сечения пирамиды
- Назначение и применение сечения пирамиды
- Сферы применения полученных плоских фигур
- Преимущества использования сечения пирамиды
- 📺 Видео
Видео:Построение линии пересечения поверхности пирамиды с проецирующей плоскостьюСкачать

Что такое пирамида
По количеству боковых граней, пирамиды делятся на треугольные, четырехугольные, пятиугольные и т. д. В случае треугольной пирамиды ее основой будет треугольник. Четырехугольной пирамидой является пирамидка. В соответствии с количеством боковых граней, пирамиды могут иметь разные названия.
Также пирамиды можно классифицировать по производным фигурам, которые можно получить в результате сечения пирамиды плоскостью. В зависимости от положения плоскости относительно пирамиды, могут получиться различные фигуры – треугольники, четырехугольники, многоугольники, эллипсы и круги.
Сечение пирамиды многоугольной плоскостью может дать ромб, параллелограмм, трапецию и другие четырехугольные фигуры. Сечение пирамиды плоскостью, проходящей через апекс и основание, дает треугольник с одним углом равным 90 градусов. Если плоскость пересекает боковые грани пирамиды, то сечение будет являться треугольником с произвольными углами.
Таким образом, сечение пирамиды плоскостью может приводить к разным плоским фигурам в результате.
| Плоскость сечения | Результат |
|---|---|
| Многоугольная плоскость | Ромб, параллелограмм, трапеция и др. |
| Плоскость через апекс и основание | Треугольник с одним углом равным 90 градусов |
| Плоскость, пересекающая боковые грани | Треугольник с произвольными углами |
Описание понятия «пирамида»
Пирамиды можно классифицировать по форме и количеству граней. Если они имеют треугольное основание и все боковые грани — также треугольники, то такая пирамида называется тетраэдром. Если основание пирамиды — четырехугольник, а все боковые грани — треугольники, то это пирамида с четырьмя гранями, или гексаэдр (сущность изображена на кубе).
Пирамиды широко используются в архитектуре, математике, физике, геометрии. Например, одним из самых известных примеров пирамиды является пирамида Хеопса в Египте, которая была построена около 2600 года до нашей эры и является одной из Семи чудес света.
Описание понятия «пирамида» является важным для понимания и изучения геометрии и ее применения в реальной жизни.
Главные характеристики пирамиды
Пирамида имеет несколько характеристик, которые являются её главными параметрами. Вот некоторые из них:
| Название | Описание |
| Высота | Расстояние между вершиной пирамиды и плоскостью, в которой находится основание |
| Основание | Плоская фигура, образующая нижнюю часть пирамиды |
| Боковые грани | Треугольные фигуры, образующие боковую часть пирамиды |
| Периметр основания | Сумма длин всех сторон основания пирамиды |
| Апофема основания | Расстояние от центра основания до середины любой из сторон основания пирамиды |
| Объём | Количество пространства, занимаемого пирамидой |
| Площадь основания | Площадь плоской фигуры, являющейся основанием пирамиды |
| Полная площадь | Сумма площадей всех граней пирамиды |
Эти характеристики определяют форму и размеры пирамиды, а также её геометрические свойства. Таким образом, изучение главных характеристик пирамиды позволяет более подробно анализировать и описывать эту геометрическую фигуру.
Видео:№55,б Пересечение пирамиды плоскостью общего положенияСкачать

Сечение пирамиды
Сечение пирамиды — это плоская фигура, которую можно получить, пересекая пирамиду плоскостью. В зависимости от угла наклона плоскости относительно пирамиды, сечение может представлять собой различные фигуры.
Если плоскость пересекает основание пирамиды, то сечение будет иметь форму, аналогичную основанию. Например, если основание пирамиды — квадрат, то и сечение будет квадратом.
Если плоскость проходит через боковые грани пирамиды, то сечение будет представлять собой многоугольник, имеющий количество сторон и форму, соответствующую форме боковой грани. Например, если боковая грань пирамиды — треугольник, то и сечение будет треугольником.
Если плоскость пересекает вершину пирамиды, то сечение будет иметь форму, аналогичную вершине. Например, если вершина пирамиды — точка, то и сечение будет точкой.
Таким образом, сечение пирамиды зависит от формы и положения плоскости, а также от формы и положения основания, боковых граней и вершины пирамиды.
Что представляет собой сечение пирамиды
Одна из наиболее распространенных фигур, которую можно получить в результате сечения пирамиды, — это треугольник. В случае, когда плоскость пересекает пирамиду вдоль одной из ее боковых граней, сечение будет иметь форму треугольника.
Однако сечения пирамид могут быть и более сложными. Если плоскость проходит через вершину пирамиды и пересекает несколько граней, в результате пересечения могут образоваться многоугольники разной формы, такие как треугольник, четырехугольник, пятиугольник и т. д.
Кроме того, в случае, когда плоскость пересекает пирамиду параллельно основанию или проходит через основание, сечение может образовать плоскую фигуру, которая будет являться усеченной или полной частью основания пирамиды.
Таким образом, сечение пирамиды может представлять собой различные плоские фигуры, включая треугольники, многоугольники и усеченные или полные части основания пирамиды.
Какими инструментами можно выполнить сечение пирамиды
Сечение пирамиды можно выполнить с помощью следующих инструментов:
- Плоскости. Используя плоскость, можно выполнить сечение пирамиды таким образом, чтобы получить плоскую фигуру.
- Пила. С помощью пилы можно провести разрезы по заданной линии, чтобы сделать сечение пирамиды.
- Лазерный резак. Современные технологии позволяют использовать лазерный резак для получения четких и точных сечений пирамиды.
- 3D-принтер. С помощью 3D-принтера можно создавать модели пирамиды и выполнять сечения с высокой точностью.
Выбор инструмента зависит от цели сечения пирамиды и доступных ресурсов. Важно учесть требуемую точность сечения, материал пирамиды и особенности выбранного инструмента. Обратитесь к специалистам, чтобы выбрать подходящий инструмент для выполнения сечения пирамиды.
Видео:Комплексный чертеж усеченной 5-гранной пирамидыСкачать

Какую плоскую фигуру можно получить в результате
Сечение пирамиды может представлять разнообразные плоские фигуры в зависимости от угла наклона и формы пирамиды. Рассмотрим несколько вариантов.
| Форма пирамиды | Получаемая фигура |
|---|---|
| Квадратная пирамида | Квадрат |
| Пирамида с прямоугольным основанием | Прямоугольник |
| Треугольная пирамида | Треугольник |
| Пирамида с многоугольным основанием | Многоугольник |
| Цилиндрическая пирамида | Эллипс |
Итак, сечение пирамиды может быть представлено различными плоскими фигурами, включая квадрат, прямоугольник, треугольник, многоугольник и эллипс. Форма получаемой фигуры будет зависеть от формы и угла наклона пирамиды.
Описание возможных фигур
Исходя из сечения пирамиды, можно получить различные плоские фигуры в результате. В зависимости от положения секущей плоскости относительно вершины пирамиды и формы самой пирамиды, возможны такие фигуры, как треугольник, прямоугольник, многоугольник, трапеция и другие.
Если секущая плоскость проходит через вершину пирамиды и параллельна основанию, то получается треугольник. Если секущая плоскость пересекает ребра пирамиды и параллельна одной из граней, то получается прямоугольник. Если секущая плоскость пересекает ребра пирамиды и не параллельна ни одной из граней, то получается многоугольник. Если секущая плоскость параллельна одной из граней пирамиды, но не пересекает ее ребра, то получается трапеция.
Таким образом, сечение пирамиды может создавать самые разнообразные плоские фигуры, в зависимости от взаимного положения пирамиды и секущей плоскости.
Примеры плоских фигур, полученных в результате сечения пирамиды
Сечение пирамиды может приводить к получению разнообразных плоских фигур, в зависимости от угла и положения секущей плоскости.
Некоторые из примеров включают в себя:
1. Треугольник
Если секущая плоскость пересекает вершину пирамиды и одну из ее боковых граней, то в результате сечения получается треугольник.
2. Прямоугольник
Если секущая плоскость параллельна основанию пирамиды, то в результате сечения можно получить прямоугольник.
3. Параллелограмм
При сечении пирамиды плоскостью, которая не параллельна основанию, возникает параллелограмм.
4. Трапеция
Если плоскость сечения параллельна одной из боковых граней и пересекает диагональ пирамиды, то в результате сечения получается трапеция.
5. Эллипс
При сечении пирамиды плоскостью, которая пересекает вершину и боковые грани, но не пересекает основание, можно получить эллипс.
Эти примеры только некоторые из множества возможных плоских фигур, которые могут быть получены при сечении пирамиды. Важно учитывать угол и положение секущей плоскости для получения конкретной фигуры.
Видео:Лекция 5 Задача 4Скачать
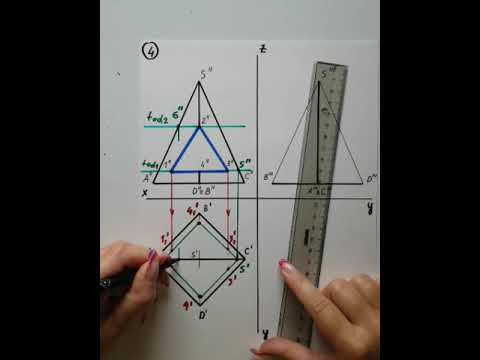
Назначение и применение сечения пирамиды
Применение сечения пирамиды широко применимо в различных областях науки и практики. Одной из основных областей, в которых сечение пирамиды находит применение, является архитектура и строительство. Архитекторы и инженеры используют сечения пирамиды для анализа и проектирования зданий, чтобы определить форму и размеры различных элементов, таких как стены, потолки и крыши.
Сечение пирамиды также находит применение в геодезии и картографии. Геодезисты и картографы используют сечения пирамиды для создания карт и планов местности. С помощью сечения пирамиды можно определить высоту точек местности, а также создать профили и разрезы ландшафтных объектов.
Кроме того, сечение пирамиды применяется в трехмерной графике и компьютерной графике. Графические дизайнеры и аниматоры используют сечения пирамиды для создания объемных моделей и анимаций различных объектов.
В искусстве и дизайне сечение пирамиды также является важным инструментом. Художники и дизайнеры могут использовать сечения пирамиды для создания интересных и оригинальных композиций, играя с формой и пространством.
| Область применения | Пример |
|---|---|
| Архитектура | Анализ формы и размеров зданий |
| Геодезия | Определение высот точек местности |
| Графика | Создание трехмерных моделей и анимаций |
| Искусство | Создание оригинальных композиций |
Сферы применения полученных плоских фигур
Полученные плоские фигуры, такие как треугольники, квадраты или прямоугольники, имеют широкие сферы применения в различных областях.
В строительстве плоские фигуры используются для расчета площади поверхности, требуемой для покрытия стен, полов или крыш. Они также помогают инженерам и архитекторам разрабатывать дизайны зданий и сооружений.
В геометрии полученные плоские фигуры являются основой для изучения различных свойств и закономерностей. Они используются при решении различных задач, например, вычисления периметра или нахождения площади фигуры.
В образовательных целях полученные плоские фигуры широко используются при обучении геометрии и математике. Они помогают учащимся развивать навыки анализа и логического мышления.
Также полученные плоские фигуры могут использоваться в дизайне, искусстве и графике для создания интересных и привлекательных композиций. Они являются элементами для создания геометрических узоров или шаблонов.
В итоге, использование полученных плоских фигур простирается на множество сфер человеческой деятельности, начиная от строительства и заканчивая образованием и искусством.
Преимущества использования сечения пирамиды
Использование сечения пирамиды имеет несколько преимуществ:
| 1. | Упрощение анализа и изучения геометрических фигур. Сечение позволяет получить плоскую фигуру, которую легче изучать и анализировать. |
| 2. | Возможность построения качественных и эффективных моделей. Сечение пирамиды позволяет создавать точные модели различных геометрических фигур, облегчая их дальнейшее изучение. |
| 3. | Упрощение вычислений. При использовании сечения пирамиды возможны более простые и понятные вычисления площади и объема полученной плоской фигуры. |
| 4. | Удобство для применения в различных научных и инженерных областях. Сечение пирамиды широко используется в различных научных и инженерных областях, таких как архитектура, строительство, дизайн и другие. |
Эти преимущества делают сечение пирамиды полезным инструментом при работе с геометрическими фигурами.
📺 Видео
Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Пересечение многогранников. Пирамида с призматическим вырезом.Скачать

Раевская. Наглядное представление тел в пространстве. 6 классСкачать

Шестиугольная пирамида.Ортогональные и изометрическая проекции.Урок31.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Построение линии пересечения поверхностей методом СЕКУЩИХ ПЛОСКОСТЕЙСкачать

Пересечение пирамиды плоскостьюСкачать

2 6 1 сечение конуса плоскостьюСкачать

Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Пересечение пирамиды с призмойСкачать
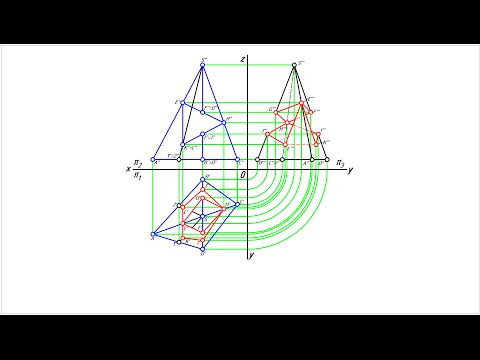
Проектирование.Изображение фигур в пространстве.Часть 1.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Начертательная геометрия. 14 урок. Пересечение пирамиды плоскостью общего положенияСкачать
