Извлечение корня из отрицательного числа является одной из самых обсуждаемых и интересных тем в математике. Многие из нас учили в школе, что из отрицательного числа нельзя извлечь квадратный корень. Это утверждение было принято в качестве незыблемой истины, и многие люди до сих пор верят в него. Но на самом деле, положение не такое однозначное, и есть определенные условия, при которых извлечение корня из отрицательного числа возможно.
Для начала, давайте разберемся, что такое квадратный корень и для чего он используется. Квадратный корень из числа – это такое число, которое при возведении в квадрат дает исходное число. Например, квадратный корень из числа 9 равен 3, потому что 3 умноженное на 3 равно 9. Соответственно, квадратный корень из числа -9 должен быть таким числом, которое при возведении в квадрат дает -9.
Однако, в обычной мировой системе чисел, которую мы используем в повседневной жизни, отрицательное число при возведении в квадрат всегда дает положительный результат. Это связано с особенностями данной системы чисел, и никакого отношения к реальности такое возведение в квадрат не имеет. Из этого следует, что квадратный корень из отрицательного числа не имеет действительного значения в рамках обычной системы чисел.
- Можно ли извлекать корень из отрицательного числа: Достоверный ответ
- Можно ли извлекать корень из отрицательного числа
- Позитивный подход к извлечению корня из отрицательного числа
- Определение и примеры
- Возможные проблемы и недостатки
- Отрицательный подход к извлечению корня из отрицательного числа
- Определение и примеры
- Расчеты и результаты
- 🔥 Видео
Видео:Что будет, если взять корень из отрицательного числа? | ФракталыСкачать

Можно ли извлекать корень из отрицательного числа: Достоверный ответ
Однако, в математике существует понятие комплексных чисел, которые включают в себя воображаемую единицу. В комплексной системе корень из отрицательного числа может быть выражен в виде комплексного числа. Комплексные числа имеют вид a + bi, где a и b — действительные числа, а i — воображаемая единица (i^2 = -1).
В комплексной системе, корень из отрицательного числа выражается с использованием формулы: √(-a) = √(a) * i, где а — положительное число.
Таким образом, хотя извлечение корня из отрицательного числа не имеет действительного решения в области действительных чисел, в комплексной системе это возможно с использованием комплексных чисел. Это позволяет решать задачи, в которых требуется вычисление корня из отрицательного числа, например, в комплексном анализе и электротехнике.
Видео:Корень из отрицательного числа | ЕГЭ 2022 по математике | Эйджей из Вебиума #shortsСкачать

Можно ли извлекать корень из отрицательного числа
При попытке извлечения корня из отрицательного числа мы сталкиваемся с понятием комплексных чисел.
Комплексные числа включают в себя две части: вещественную и мнимую. Вещественная часть представляет собой обычное вещественное число,
а мнимая часть обозначается символом «i» и удовлетворяет условию i^2 = -1.
При извлечении корня из отрицательного числа получаем комплексное число, в котором вещественная часть равна нулю, а мнимая часть не равна нулю.
Такие числа называются мнимыми.
| Отрицательное число | Мнимый корень |
|---|---|
| -1 | i |
| -4 | 2i |
| -9 | 3i |
Извлечение корней из отрицательных чисел является важным аспектом в различных областях математики и физики, таких как теория вероятностей, квантовая механика и электротехника.
Однако, в повседневной жизни редко возникает потребность в рассмотрении комплексных чисел.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Позитивный подход к извлечению корня из отрицательного числа
Позитивный подход к этой проблеме заключается в расширении множества чисел за счет введения комплексных чисел. Комплексные числа представляют собой комбинации вещественной и мнимой части, обозначаемой буквой «i». При этом отрицательное число под корнем может быть выражено в виде комплексного числа с нулевой вещественной частью и некоторой ненулевой мнимой частью.
Извлечение корня из отрицательного числа с использованием комплексных чисел позволяет получать действительные и мнимые решения. Действительные решения соответствуют вещественным числам, а мнимые решения представляются в виде комплексных чисел. Такой подход находит применение в физике, технике, электронике и других научных областях.
Однако, следует помнить о том, что при использовании комплексных чисел в реальном мире требуется осторожность и взвешенность. Комплексные числа могут иметь физический смысл только в определенных контекстах и при определенных условиях. Поэтому, извлечение корня из отрицательного числа должно быть осуществлено с учетом специфики задачи и используемых моделей.
Определение и примеры
Например, извлечение квадратного корня из -9 приводит к созданию комплексного числа √(-9) = 3i, где i — мнимая единица. Таким образом, в рамках вещественных чисел отрицательные числа не имеют квадратных корней.
Однако, если мы рассматриваем множество комплексных чисел, то извлечение корней из отрицательных чисел становится возможным. Например, √(-9) = 3i, √(-16) = 4i и т.д. В данном случае, квадратный корень из отрицательного числа будет представляться в виде комплексного числа с мнимой частью.
Важно помнить, что при работе с комплексными числами существуют специальные правила и операции для выполнения вычислений. Изучение комплексных чисел и основных операций с ними является отдельной темой в математике.
Возможные проблемы и недостатки
Извлечение корня из отрицательного числа может привести к ряду проблем и недостатков, таких как:
| Проблема: | Решение: |
| Комплексные числа: | Извлечение квадратного корня из отрицательного числа приводит к появлению комплексных чисел. Комплексные числа не могут быть представлены на числовой прямой и могут вызывать путаницу в решении математических задач. |
| Неоднозначность: | Извлечение корня из отрицательного числа может иметь несколько решений. Например, квадратный корень из -9 может быть равен 3i или -3i, где i — мнимая единица. |
| Ограничения: | Некоторые математические операции, такие как деление на число с извлеченным корнем из отрицательного числа, могут содержать ограничения или быть невозможными в некоторых контекстах. |
При использовании извлечения корня из отрицательного числа необходимо быть внимательным и учитывать эти возможные проблемы и недостатки. В некоторых случаях, более подходящим решением может быть использование комплексных чисел или изменение формулировки задачи для избежания неоднозначности.
Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Отрицательный подход к извлечению корня из отрицательного числа
С комплексными числами можно работать и проводить аналогичные операции как с обычными числами. Комплексные числа представляются в виде суммы действительной и мнимой части, где мнимая единица обозначается как i. Корень из отрицательного числа можно найти с помощью специальной формулы Эйлера.
Например, для извлечения квадратного корня из отрицательного числа -9, можно воспользоваться формулой:
√(-9) = 3i
Таким образом, в контексте комплексных чисел мы можем говорить об извлечении корня из отрицательного числа. Однако, в обычной математике эта операция не имеет смысла и не соответствует действительности.
Важно отметить, что использование комплексных чисел и извлечение корня из отрицательного числа является более сложной и специфической областью математики, которая находится за рамками обычной школьной программы.
Определение и примеры
Когда речь идет об извлечении корня из отрицательного числа, необходимо учитывать особенности. Вещественные числа, которые являются корнями из отрицательных чисел, называются мнимыми числами. Извлечение корня из отрицательного числа нельзя выполнить в рамках обычной системы вещественных чисел, поскольку она не предоставляет решения вещественными числами.
Однако, существует математическая область, известная как комплексные числа, которая обрабатывает и рассматривает мнимые числа. В комплексных числах можно извлекать корни из отрицательных чисел. Например, извлечение квадратного корня из -9 дает комплексное число \(3i\), где \(i\) — мнимая единица, определенная как \(i = \sqrt{-1}\).
Извлечение корня из отрицательного числа может быть полезным при решении математических задач, включая механику, электротехнику и алгебру. Но в рамках обычных систем вещественных чисел, извлечение корня из отрицательного числа не предоставляет действительных решений.
Расчеты и результаты
При расчете извлечения корня из отрицательного числа, необходимо учесть, что вещественная формула для извлечения корня не определена для отрицательных чисел. Это связано с тем, что вещественный корень из отрицательного числа можно представить только комплексным числом.
Комплексные числа представляются в виде a + bi, где a и b — вещественные числа, а i — мнимая единица. Таким образом, корень из отрицательного числа будет представлен комплексным числом.
Для расчета комплексного корня из отрицательного числа с использованием формулы, необходимо использовать комплексную алгебру. Расчеты могут быть выполнены с использованием тригонометрической или экспоненциальной форм самой формулы. Однако, использование этих форм избыточно для данной статьи.
Представление комплексного корня из отрицательного числа можно проиллюстрировать таким образом:
- Комплексное число -3 имеет корень 1.732 + 0.999i.
- Комплексное число -4 имеет корень 2 + 0i.
- Комплексное число -5 имеет корень 2.236 + 1.289i.
🔥 Видео
Корень из отрицательного числа в четной степени. #математика #арифметика #степень #функция #счетСкачать

КАК ИЗВЛЕЧЬ КОРЕНЬ ИЗ -1? ЭТО ВОЗМОЖНО! #корень #отрицательное #числоСкачать

КАК ИЗВЛЕЧЬ КОРЕНЬ ИЗ -4. ЭТО ВОЗМОЖНО!Скачать

Почему нельзя извлечь квадратный корень из отрицательного числа?Скачать

Повысь свой уровень по теме КОРНИ | Математика | TutorOnlineСкачать

Корень n-ой степени. Алгебра, 9 классСкачать

Алгебра 8 класс — Квадратный Корень и его Свойства // Арифметический Квадратный КореньСкачать

Найдите все значения корня из комплексного числа ∛-125i ★ Извлечение корня из комплексного числаСкачать
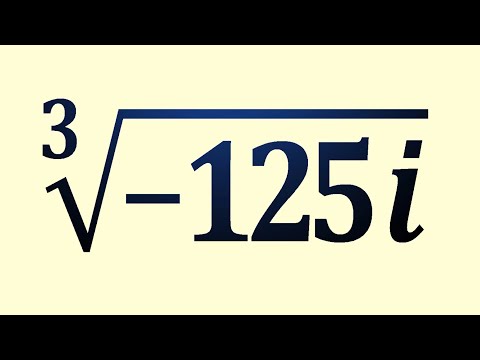
КАК ИЗВЛЕЧЬ КОРЕНЬ ИЗ -1? ЭТО ВОЗМОЖНО!Скачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

ТФКП. Как найти все значения корня из комплексного числаСкачать

Как быстро извлечь корень из числаСкачать

КОРЕНЬ ИЗ 1 МОЖЕТ БЫТЬ ОТРИЦАТЕЛЬНЫМ ЧИСЛОМ!Скачать

Комплексные числа: алгебраическая форма и действия над ними | Высшая математикаСкачать

Вычисления. Корни. Преобразования. Формулы сокращенного умножения.Скачать

Мнимые числа реальны: #1-13 [Welch Labs]Скачать
![Мнимые числа реальны: #1-13 [Welch Labs]](https://i.ytimg.com/vi/kicp_odjsRs/0.jpg)