Деление на ноль — одно из наиболее интересных и спорных понятий в математике. Как же возможно поделить на что-то, чего не существует? Возникает множество вопросов и дискуссий относительно этой темы, и поэтому понимание ее сути является важным для всех, кто изучает математику.
В этой статье мы постараемся разобраться в особенностях деления на ноль и его последствиях. Во-первых, стоит отметить, что в классической математике, основанной на аксиомах, деление на ноль считается неопределенным значением. Это означает, что решение такой операции принято не давать, поскольку оно противоречит логике и порождает противоречивые результаты.
Однако, в других математических системах, таких как действительные или комплексные числа, введены специальные правила, позволяющие оперировать делением на ноль. Например, в расширенном поле комплексных чисел существует бесконечность и неопределенность. Это ставит под вопрос обоснованность и такую глубокую операцию в реальной жизни.
- Причины невозможности деления на ноль
- Аксиоматика чисел
- Определение деления
- Математическая интуиция
- Последствия деления на ноль
- Несуществование обратного элемента
- Обнаружение ошибок
- Расширенная числовая система
- Бесконечность
- Специальное значение
- Влияние на математические применения
- Моделирование реальности
- 📹 Видео
Видео:Ты МОЖЕШЬ делить на ноль! | РЕАЛЬНАЯ ПРИЧИНАСкачать

Причины невозможности деления на ноль
1. Нарушение основных математических правил.
Математика базируется на ряде строгих правил, которые определяют корректное выполнение различных операций. Одним из таких правил является запрет на деление числа на ноль. Если бы было возможно делить на ноль, это привело бы к нарушению этих правил и противоречию в самой математической системе.
2. Отсутствие определенного результата.
Одной из ключевых характеристик деления является определенность результата. Если мы разделяем число на некоторое другое число, мы ожидаем получить точный результат. Однако, при делении на ноль не существует единственного значения, которое можно было бы считать ответом. Вместо этого, результат деления на ноль неопределен и не может быть выражен конкретным числом.
3. Противоречие в математических уравнениях.
Деление на ноль может привести к противоречию в уравнениях и неравенствах. Например, если мы разделим число на ноль в уравнении x/0 = 5, мы не сможем найти единственное значение x, которое удовлетворяет такому уравнению. Это связано с тем, что деление на ноль нарушает правила алгебры и приравнивает некоторое число к бесконечности.
В целом, деление на ноль не имеет смысла в математике и противоречит основным принципам и правилам этой науки. Поэтому, любые попытки разделить число на ноль будут невозможны и неопределенны.
Аксиоматика чисел
Аксиоматика чисел строится на основе нескольких основных принципов:
- Существование нуля: существует число ноль, обозначаемое символом «0», которое не является ни положительным, ни отрицательным числом.
- Существование единицы: существует число один, обозначаемое символом «1», которое является наименьшим натуральным числом.
- Принцип индукции: если для некоторого утверждения верно, что оно выполняется при нуле и что оно выполняется при любом натуральном числе, то оно выполняется при всех натуральных числах.
- Законы операций: для любых двух чисел a и b определены операции сложения (+) и умножения (·), которые обладают свойствами коммутативности, ассоциативности и дистрибутивности.
- Принцип порядка: для любых двух чисел a и b одно из следующих утверждений верно: a < b, a = b или a > b. Это принцип устанавливает отношение порядка между числами.
- Принцип архимедовости: для любых двух положительных чисел a и b всегда можно найти такое натуральное число N, что произведение числа a на N будет больше числа b.
Определение деления
| Делимое | Делитель | Частное |
| a | b | a / b или a : b |
Делимое — это число, которое будет делиться на другое число (делитель). Делитель — это число, на которое делимое будет делиться. Частное — это результат деления, то есть сколько раз делимое содержит делитель.
Операция деления может быть выполнена только в том случае, когда делитель не равен нулю. Если делитель равен нулю, то деление становится невозможным, так как нельзя разделить что-либо на ноль.
Если деление на ноль в математике было бы возможно, то это привело бы к неоднозначным и неправильным результатам. Например, если попытаться разделить число на ноль, то получится бесконечность или «неопределенное» значение. Это противоречит логике и правилам математики.
Математическая интуиция
Математическая интуиция позволяет ученым делать предположения, выдвигать гипотезы и находить новые способы решения проблем. Она основана на опыте, накопленном в области математики, и интуитивном понимании ее основных принципов.
Одним из примеров математической интуиции является понимание концепции бесконечности. В то время как формальные математические доказательства требуют сложных операций и символов, интуитивное понимание бесконечности позволяет ученым представить ее как нечто неограниченное и неизмеримое.
Математическая интуиция также помогает в понимании абстрактных концепций, таких как множества и функции. С помощью интуиции математик может представить себе, как эти концепции взаимосвязаны и влияют друг на друга.
Однако, математическая интуиция не всегда является надежным источником знания. Возможны случаи, когда интуитивное решение оказывается ошибочным или не полностью соответствующим формальным доказательствам. Поэтому в математике широко используются строгие логические методы для проверки и подтверждения интуитивных решений.
Видео:Деление на ноль. Объяснение математического смысла.Скачать

Последствия деления на ноль
Неопределенность
Если мы попытаемся разделить число на ноль, результатом этой операции будет неопределенность. Это означает, что мы не можем однозначно определить значение деления на ноль, так как математические правила не предусматривают такую операцию.
Бесконечность
Иногда, деление на ноль может привести к бесконечности. Например, если мы разделим число единица на очень маленькое число, близкое к нулю, результатом будет число, стремящееся к положительной или отрицательной бесконечности.
Аномалии в вычислениях
Попытка деления на ноль может вызвать аномалии в вычислениях. Например, если мы попытаемся разделить любое число на ноль в компьютерной программе, это может привести к ошибке или сбою программы, так как компьютеры не могут обработать деление на ноль.
В целом, деление на ноль является математической ошибкой, которая может привести к неопределенным результатам и аномалиям. Поэтому в математике и в программировании необходимо избегать деления на ноль, чтобы избежать возможных проблем и ошибок.
Несуществование обратного элемента
Для всех чисел, кроме нуля, обратный элемент существует. Например, для числа 2 обратным элементом будет 0,5, так как 2 умноженное на 0,5 дает 1, то есть нейтральный элемент.
Однако для нуля обратного элемента не существует. Если мы попытаемся разделить любое число на ноль, мы не сможем получить никакого результата. Это происходит потому, что не существует такого числа, при умножении на которое нуль даст единицу.
Поэтому попытка деления на ноль приводит к математической неопределенности и некорректности операции. Такое деление не имеет смысла и не может быть выполнено.
В результате, деление на ноль рассматривается в математике как недопустимая операция. При попытке выполнить такую операцию, получается неопределенность или противоречие, что мешает продолжению вычислений и приводит к математической ошибке. Поэтому, в целях обеспечения строгости и верности математических выкладок, деление на ноль является недопустимой операцией.
Обнаружение ошибок
Одним из показателей возможной ошибки является появление бесконечности в результате деления числа на ноль. Если на самом этапе вычислений обнаруживается попытка деления на ноль, необходимо прервать выполнение выражения и выдать ошибку пользователю.
Дополнительным инструментом обнаружения ошибок может служить проверка знаменателя перед выполнением деления. Если знаменатель равен нулю, то деление не может быть произведено и следует также выдать сообщение об ошибке.
Обнаружение ошибок деления на ноль является важной составляющей при разработке программ, связанных с математическими расчетами. Это позволяет гарантировать корректность результатов и надежность программного обеспечения.
Видео:Почему нельзя делить на ноль? – Алексей Савватеев | Лекции по математике | НаучпопСкачать

Расширенная числовая система
В математике, существует расширенная числовая система, которая позволяет обрабатывать деление на ноль. Эта система называется расширенными числами или числами с бесконечностью.
В расширенной числовой системе, обычные действия, такие как сложение и умножение, выполняются так же, как и в обычной арифметике. Однако, при делении на ноль мы получаем бесконечность. Такое деление обозначается символом $\frac{1}{0}$, где числитель равен 1, а знаменатель равен нулю. Бесконечность обозначается символом ∞.
Расширенная числовая система имеет свои особенности. Например, при сложении числа с бесконечностью, результат остается бесконечным, но с противоположным знаком. То есть $∞ + a = -∞$, где $a$ — любое конкретное число.
Также, при умножении числа на бесконечность, результат будет бесконечностью, но со знаком, зависящим от знака числа. Например, $∞ \cdot a = ∞$, если $a > 0$, и $∞ \cdot a = -∞$, если $a < 0$.
Расширенная числовая система позволяет проводить арифметические операции с бесконечностью и делить на ноль, но важно помнить, что эта система имеет свои особенности и отличается от обычной арифметики.
Бесконечность
Бесконечность представляет собой идею о том, что число или значение могут быть неограниченно большими или маленькими.
В математике бесконечность обычно представляется символом ∞. Она может использоваться для обозначения различных концепций, таких как бесконечно удаленные точки на числовой прямой или бесконечно малые значения, которые стремятся к нулю.
Деление на ноль может породить понятие «бесконечности», так как результат такого деления может быть неограниченно большим, в зависимости от контекста. Например, если мы делим число на очень маленькое число, результат будет очень большим, почти бесконечным.
Однако, математика не позволяет полноценно работать с бесконечностями или делить на ноль без специальных правил. Введение таких правил и символов, как «бесконечность», имеет свои ограничения и требует аккуратного и строго определенного подхода.
Таким образом, бесконечность является важным понятием в математике, но само деление на ноль и связанные с ним последствия требуют специального подхода и правил для корректной работы с этими понятиями.
Специальное значение
Математики используют два специальных значения для обозначения бесконечности в разных направлениях. Если результат деления положительного числа на ноль, то он будет равен положительной бесконечности (∞), а если результат деления отрицательного числа на ноль, то он будет равен отрицательной бесконечности (-∞).
Наличие специального значения бесконечности позволяет формализовать анализ функций и уравнений, в которых возможно деление на ноль. Оно упрощает математические выкладки и позволяет получать точные результаты в этих случаях.
Однако, деление на ноль является особым случаем, и его не следует рассматривать как обычную операцию. Оно может привести к непредсказуемым последствиям и ошибкам в реальных вычислениях. Поэтому в программировании и инженерных расчетах важно учитывать возможность деления на ноль и предусмотреть соответствующие проверки и обработку таких ситуаций.
Важно помнить:
- Деление на ноль является неопределенной операцией.
- Специальные значения бесконечности используются для обозначения результата деления на ноль.
- Бесконечность имеет два направления: положительное и отрицательное.
- Использование деления на ноль требует особой осторожности и проверок в программировании и расчетах.
Специальное значение бесконечности позволяет формализовать математические операции, в которых возможно деление на ноль. Но в реальных вычислениях необходимо учитывать эти случаи и принимать меры для предотвращения ошибок.
Видео:✓ Можно ли делить на ноль? | Ботай со мной #019 | Борис ТрушинСкачать

Влияние на математические применения
Во-первых, понимание деления на ноль позволяет изучать и решать разнообразные математические задачи. В некоторых математических областях, таких как теория чисел и алгебра, деление на ноль имеет особое значение и играет важную роль в определении и свойствах различных математических объектов.
Во-вторых, деление на ноль имеет широкое применение в научных и инженерных расчетах. Например, в физике и инженерии часто возникают ситуации, когда требуется учесть деление на ноль для получения точных результатов расчетов. Без понимания и учета деления на ноль эти расчеты были бы невозможны или не точны.
Однако, без должного понимания и ограничений на деление на ноль, могут возникать ошибки и проблемы в математических применениях. Например, деление на ноль может привести к неопределенности или некорректным результатам. Поэтому в математике существуют определенные правила и условия, которые ограничивают или запрещают деление на ноль.
В целом, понимание деления на ноль имеет важное значение для математики и ее применений. Это позволяет углубляться в изучение различных математических областей, решать сложные проблемы и получать точные результаты в научных и инженерных расчетах.
Моделирование реальности
Деление на ноль является неопределенной операцией, которая не имеет однозначного результата. В математике, деление на ноль запрещено, поскольку это противоречит основным правилам и определениям.
Однако, в некоторых специальных случаях, деление на ноль может быть допустимым в рамках так называемой «расширенной числовой системы». Например, в математике с комплексными числами, существует определенное правило для деления на ноль.
Во многих физических моделях и уравнениях, возникающих при изучении реального мира, деление на ноль может привести к неожиданным или нефизичным результатам. Например, деление на ноль может привести к бесконечности или противоречить законам сохранения энергии и массы.
При моделировании реальности, важно учитывать ограничения и проблемы, связанные с делением на ноль. Использование подходящих методов и техник моделирования позволяет учесть эти ограничения и получить более реалистичные и надежные результаты.
Таким образом, деление на ноль является одной из проблем и ограничений, с которыми сталкиваются при моделировании реальности. В понимании причин и последствий этой операции, математика играет важную роль в изучении и построении моделей, которые помогают нам лучше понять и описать окружающий нас мир.
📹 Видео
Тебе НЕЛЬЗЯ делить на ноль! | РЕАЛЬНАЯ ПРИЧИНАСкачать
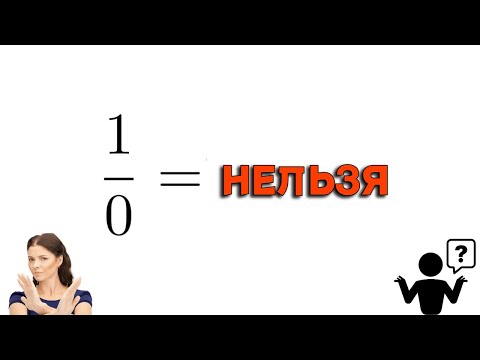
Почему 0 в степени 0 равно 1?Скачать

В реале кто-то (не)прав! Деление 0 на 0Скачать

Почему нельзя ДЕЛИТЬ НА НОЛЬ? (Артур Шарифов)Скачать

Математика это не ИсламСкачать

КОГДА ДЕЛИТЬ НА НОЛЬ МОЖНО, А КОГДА - НЕЛЬЗЯ? | НаучпопСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

ПОЧЕМУ НЕЛЬЗЯ ДЕЛИТЬ НА НОЛЬ?Скачать

10 глупых вопросов МАТЕМАТИКУ | Алексей СавватеевСкачать

Почему 2 + 2 = 4? Отвечает математик Алексей Савватеев | Математика для всех 😉Скачать

Математика 2 класс (Урок№53 - Конкретный смысл действия деление.)Скачать

🔶 Почему нельзя делить на ноль? [TED-Ed на русском]Скачать
![🔶 Почему нельзя делить на ноль? [TED-Ed на русском]](https://i.ytimg.com/vi/6x6qg-vqddI/0.jpg)
Проблемы с нулём - NumberphileСкачать

Интересная математика с юмором. Почему нельзя делить на ноль?Скачать

Алексей Савватеев | Почему математика может все? Ну, почти...Скачать

Слабое место математики: можно ли доказать всё, что истинно? [Veritasium]Скачать
![Слабое место математики: можно ли доказать всё, что истинно? [Veritasium]](https://i.ytimg.com/vi/jP3ceURvIYc/0.jpg)