Классификация точек разрыва функции виды и особенности (4 видео)

В математике точки разрыва функции играют важную роль в понимании и анализе ее поведения. Точкой разрыва называется значение функции, в котором она теряет свою определенность или становится несобственной.

Существует несколько видов точек разрыва функции, которые можно классифицировать по их особенностям. Одним из наиболее распространенных видов является точка изолированного разрыва. В таких точках функция может быть не определена, либо иметь различные значения слева и справа от этой точки. Точка изолированного разрыва может возникать при наличии различных особенностей функции, таких как разрывы первого или второго рода.

Разрыв первого рода возникает в точке, где функция имеет конечные или бесконечные пределы как справа, так и слева от данной точки, но эти пределы не совпадают. Такой разрыв может произойти, например, при наличии вертикальной асимптоты или разрыва второго рода.

Разрыв второго рода возникает в точке, где функция имеет хотя бы один из пределов равным бесконечности. В этой точке функция либо не имеет предела, либо имеет предел, равный плюс или минус бесконечности. Разрыв второго рода может быть вызван наличием вертикальной асимптоты, разрыва первого рода или другими особенностями функции.

Содержание

Точки разрыва функции
Что такое точка разрыва функции
Почему возникают точки разрыва функции
Классификация точек разрыва функции
Разрывы первого рода
Разрывы второго рода
Точки разрыва монотонности
Особенности точек разрыва функции
Функциональная односторонность
Возможность асимптотического поведения
Влияние на производные функции
🎦 Видео

Видео:Непрерывность функции и точки разрыва функцииСкачать

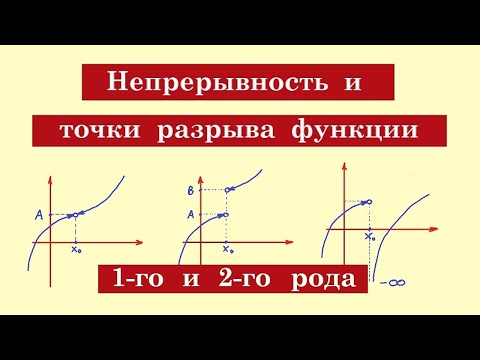
Точки разрыва функции

Первый тип точки разрыва — точка разрыва первого рода. В такой точке функция имеет пределы слева и справа, но значение функции в этой точке не определено. Можно сказать, что функция «расходится» в этой точке. Например, функция f(x) = 1/x имеет точку разрыва первого рода в x = 0.

Второй тип точки разрыва — точка разрыва второго рода. В такой точке функция имеет пределы слева и справа, но значения пределов не равны. То есть, функция «осциллирует» в этой точке. Например, функция f(x) = sin(1/x) имеет точку разрыва второго рода в x = 0.

Третий тип точки разрыва — особые точки. В такой точке функция не имеет ни предела слева, ни предела справа. Это может происходить, например, когда функция имеет вертикальную асимптоту или разрыв второго рода. Например, функция f(x) = 1/(x — 2) имеет особую точку в x = 2.

Точки разрыва функции имеют важное значение при изучении ее свойств и поведения. В зависимости от типа точки разрыва, у функции могут быть различные особенности, такие как коносность, непрерывность или прыжки значений. Изучение точек разрыва помогает понять, как функция ведет себя вблизи этих точек и как ее график строится.

Важно: Изучение точек разрыва функции требует анализа пределов и свойств функции в окрестности этих точек.

Что такое точка разрыва функции

Разрыв первого рода происходит, когда значение функции в точке разрыва не существует. Это может быть вызвано делением на ноль, возведением в отрицательную степень, извлечением квадратного корня из отрицательного числа и другими подобными случаями. В такой точке функция может показывать различное поведение в зависимости от направления подхода к ней.

Разрыв второго рода происходит, когда значение функции в точке разрыва неограничено или бесконечно большое. Это может произойти, например, когда функция имеет вертикальную асимптоту или приближается к бесконечности в данной точке.

Устранимый разрыв — это разрыв, который может быть устранен путем определенной корректировки функции. Например, можно внести изменения в функцию, чтобы значение в точке разрыва было определено или было внесено поправочное значение.

Понимание и классификация точек разрыва функции помогает анализировать и понимать их поведение на графике, а также исследовать характеристики функций и их свойства.

Почему возникают точки разрыва функции

Основные причины точек разрыва функции включают в себя:

Недопределенность: Если функция имеет недопределенность на определенной точке, то она будет иметь разрыв в этой точке. Например, функция с делением на ноль, где знаменатель равен нулю, будет иметь точку разрыва в этой точке.
Изменение определения: Функция может иметь разрыв, если ее определение меняется на определенных значениях аргумента. Например, функция, которая имеет определение только для положительных значений, будет иметь разрыв в нуле, так как она не определена для него.
Изменение свойств функции: Функция может иметь разрыв, если ее свойства изменяются на определенной точке. Например, функция, которая имеет разрыв в точке, где ее значение меняется с положительного на отрицательное или наоборот.

Точки разрыва функции важны для понимания ее поведения и связанных с ней математических концепций. Они могут быть использованы для классификации функций и определения их особенностей. Поэтому, изучение точек разрыва функции является важной частью математического анализа и исследования функций.

Видео:Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Классификация точек разрыва функции

Точки разрыва функции могут быть классифицированы на три основных типа: скачок, разрыв первого рода и разрыв второго рода.

Скачок — это тип точки разрыва функции, где значение функции меняется резко при приближении к этой точке. В точке скачка значение функции может меняться с одного предела на другой в зависимости от направления приближения.

Разрыв первого рода — это тип точки разрыва функции, где существуют конечные пределы слева и справа от точки, но они отличаются. Функция может иметь различные значения на левой и правой сторонах этой точки разрыва.

Разрыв второго рода — это тип точки разрыва функции, где хотя бы один из конечных пределов слева или справа стремится к бесконечности (положительной или отрицательной). Это может происходить, например, когда функция имеет вертикальную асимптоту или полюс.

Знание типа точки разрыва функции может помочь в анализе поведения функции в этой точке и понимании ее особенностей.

Разрывы первого рода

Классифицировать разрывы первого рода можно на следующие типы:

Точка разрыва излома: В этом случае функция определена в точке разрыва, но левосторонний и правосторонний пределы не существуют или не равны друг другу. Это приводит к созданию излома на графике функции.

Точка разрыва отвергнутая: В этом случае функция не определена в точке разрыва, но левосторонний и правосторонний пределы существуют и конечны. Это приводит к созданию отвергнутой точки на графике функции.

Точка разрыва разрыв в значении: В этом случае функция определена в точке разрыва, но левосторонний и правосторонний пределы существуют и конечны, причем значения пределов различны. Это приводит к созданию разрыва в значении на графике функции.

Разрывы первого рода имеют важное значение в математике и позволяют анализировать поведение функций в различных точках. Их классификация позволяет более точно определить свойства и особенности функций, что дает возможность решать более сложные задачи и применять математические методы в различных областях науки и техники.

Разрывы второго рода

Чтобы более подробно изучить разрывы второго рода, необходимо проанализировать поведение функции в точке разрыва. Обычно, для определения типа разрыва второго рода, рассматриваются пределы функции слева и справа от точки разрыва.

Если левосторонний предел функции в точке разрыва существует, но он не равен значению функции в этой точке, то существует разрыв второго рода с левой стороны. Аналогично, если правосторонний предел функции в точке разрыва существует, но он не равен значению функции в этой точке, то существует разрыв второго рода с правой стороны.

Разрывы второго рода могут быть также классифицированы на основе бесконечностей. Если значение функции в точке разрыва является бесконечностью, то разрыв называется разрывом второго рода со скачком. Если значение функции в точке разрыва конечно, но не равно пределу функции, то разрыв называется разрывом второго рода без скачка.

Разрывы второго рода могут возникать из-за различных математических особенностей и необычных свойств функций. Их изучение позволяет более глубоко понять поведение функций и определить их асимптотическое поведение вблизи точек разрыва.

Тип разрыва	Описание
Разрыв второго рода с левой стороны	Левосторонний предел функции в точке разрыва существует, но не равен значению функции в этой точке
Разрыв второго рода с правой стороны	Правосторонний предел функции в точке разрыва существует, но не равен значению функции в этой точке
Разрыв второго рода со скачком	Значение функции в точке разрыва является бесконечностью
Разрыв второго рода без скачка	Значение функции в точке разрыва конечно, но не равно пределу функции

Точки разрыва монотонности

Для функций, обладающих монотонностью (т.е. строго возрастающих или строго убывающих на заданном промежутке), особая роль играют точки разрыва монотонности.

Точка разрыва монотонности — это точка, в которой функция меняет свою монотонность. Именно в таких точках функция может переходить от возрастания к убыванию или наоборот.

При анализе функции на предмет точек разрыва монотонности необходимо учитывать следующее:

Сначала определяются значениям функции в критических точках, которые образуют границы области определения функции.
Затем изучаются поведение функции на интервалах между критическими точками.
Если функция является монотонной, это означает, что на каждом интервале между критическими точками она либо возрастает, либо убывает.
Если функция меняет свою монотонность на каком-то интервале, то в этой точке находится точка разрыва монотонности.
Точка разрыва монотонности может быть либо точкой разрыва первого рода (изменение монотонности несущественно), либо точкой разрыва второго рода (изменение монотонности существенно).

Точки разрыва монотонности играют важную роль при анализе функций, позволяя определить характер поведения функции, а также определить наличие особых точек на графике функции.

Видео:Математический анализ, 5 урок, Непрерывность функцииСкачать

Особенности точек разрыва функции

1. Скачок функции: В некоторых точках разрыва функция может иметь скачок, то есть ее значение в этой точке может быть разным с разных сторон. Например, функция может быть непрерывной слева, но не непрерывной справа, и значение функции слева и справа от этой точки будет различным.

2. Разрыв первого рода: В точках разрыва первого рода левый и правый пределы функции в этой точке существуют, но не равны друг другу. Это значит, что функция может быть непрерывной слева и непрерывной справа от этой точки, но не непрерывной в самой точке.

3. Разрыв второго рода: В точках разрыва второго рода, один из пределов функции в этой точке не существует. Он может быть бесконечным или неопределенным. Такие точки разрыва могут быть, например, вертикальными асимптотами функции.

4. Устранимый разрыв: Устранимый разрыв — это разрыв, который можно устранить, добавив или изменив значение функции в этой точке. Например, если функция имеет разрыв первого рода в точке, но значение функции в этой точке определено, то можно устранить разрыв, просто присвоив функции значение в этой точке, равное левому или правому пределу.

5. Неустранимый разрыв: Неустранимый разрыв — это разрыв, который нельзя устранить, не изменяя саму функцию. Например, если в точке разрыва первого рода значение функции не определено и ни левый, ни правый пределы не существуют, то такой разрыв неустраним.

Изучение особенностей точек разрыва функции позволяет более глубоко понять ее поведение и строение, а также применять различные методы анализа и классификации функций.

Функциональная односторонность

При функциональной односторонности в данной точке функция может обладать либо пределом слева, либо пределом справа, но не может иметь обоих пределов одновременно. В результате функция обрывается на этой точке и не имеет значения в этой точке.

Функциональная односторонность может возникать в различных ситуациях, например, когда функция становится неограниченной вблизи точки, при наличии вертикальных или особенных асимптот, или когда функция принимает бесконечное значение в данной точке, но при этом одно из односторонних пределов существует.

Определение функциональной односторонности и анализ ее особенностей позволяет провести классификацию точек разрыва функций и более полно понять их свойства и поведение в окрестности этих точек.

Возможность асимптотического поведения

При изучении точек разрыва функций важно учитывать их асимптотическое поведение. Асимптотические линии представляют собой графики функций, к которым приближается функция в пределе.

При анализе точек разрыва функций можно обнаружить асимптотическое поведение, которое может быть представлено в виде вертикальной, горизонтальной или наклонной асимптоты.

Вертикальная асимптота возникает, когда значение функции приближается к бесконечности при приближении переменной к определенному значению. График функции все ближе и ближе подходит к вертикальной прямой, но никогда не пересекает ее.

Горизонтальная асимптота возникает, когда значение функции стремится к определенному конечному числу при стремлении переменной к бесконечности или к минус бесконечности. График функции все ближе и ближе подходит к горизонтальной прямой, но никогда не пересекает ее.

Наклонная асимптота возникает, когда значение функции стремится к определенному конечному числу при стремлении переменной к бесконечности. График функции все ближе и ближе подходит к наклонной прямой, но никогда не пересекает ее.

Анализ асимптотического поведения точек разрыва функций позволяет лучше понять и описать их свойства и особенности. Такой анализ является неотъемлемой частью математического исследования функций и способствует более глубокому пониманию их поведения на бесконечности.

Влияние на производные функции

При анализе точек разрыва функции, в случае если функция имеет производную в данной точке, важно учитывать следующие аспекты:

Знак производной функции в точке разрыва. Если производная положительна, то функция увеличивается в этой точке. Если производная отрицательна, то функция убывает. Эта информация может быть полезна при решении задач оптимизации или определении экстремумов функции.
Существование предела производной функции в точке разрыва. Если предел производной существует, то функция может быть расширена до непрерывной функции путем определения значения функции в точке разрыва как предел ее значения с каждой стороны. В таком случае, производная функции можно определить на всей области определения.
Наличие разрывов производной функции в точке разрыва. Если предел производной не существует или равен бесконечности, то функция имеет разрыв второго рода в данной точке, что может привести к особым свойствам поведения функции. Например, функция может иметь числовые или асимптотические разрывы.

Таким образом, производные функции играют важную роль при анализе точек разрыва функции. Они позволяют определить направление изменения функции, наличие непрерывности и свойства поведения функции в данных точках, что в свою очередь может быть полезно для решения различных задач исследования функций.