Формулы — это составные части математического языка, которые используются для описания отношений и операций между числами, переменными и другими математическими объектами. Использование формул позволяет нам точно и однозначно передавать информацию о математических свойствах объектов и взаимосвязях между ними.
Основными элементами формулы являются числа, переменные, операции и скобки. Каждый из этих элементов выполняет свою роль в структуре формулы и определяет ее смысл и значимость. Числа представляют собой конкретные значения, которые могут быть как целыми, так и десятичными. Переменные, в свою очередь, представляют неизвестные значения, которым можно придать конкретное значение при решении формулы.
Операции — это математические действия, такие как сложение, вычитание, умножение и деление, которые позволяют комбинировать числа и переменные для получения новых значений. Скобки используются для определения порядка выполнения операций и группировки элементов формулы. Например, скобки могут задавать, какие операции должны быть выполнены первыми, чтобы получить правильный результат.
Видео:PROСТО О СЛОЖНОМ. Белки и их структуры. Биохимия №1Скачать

Важность структуры формулы
Одним из основных элементов структуры формулы является использование правильных скобок и расстановка приоритетов операций. Корректное расположение скобок помогает определить порядок выполнения операций и избежать возможных разночтений и ошибок. Кроме того, использование удобочитаемых символов и переменных в формуле также важно для ее структуры и понимания.
Структура формулы также может включать использование знаков и индексов для обозначения специфических элементов или переменных. Знаки, такие как плюс, минус, умножение и деление, помогают читателю быстро определить, какие операции выполняются в формуле. Индексы, с другой стороны, позволяют отличать разные варианты переменных или элементов.
Неверная или плохо организованная структура формулы может привести к неправильным результатам и путанице во время ее использования. Например, неправильно расставленные скобки могут привести к некорректному порядку операций и ошибкам в решении задачи. Также, нечеткое или неправильное использование символов и переменных может затруднить понимание формулы и привести к неправильному толкованию ее смысла.
В целом, правильная структура формулы является неотъемлемым элементом успешного использования математических выражений и решении задач. Четкая и логическая организация формулы помогает ее пониманию, а также повышает точность и эффективность ее применения.
Видео:Структура ДНКСкачать

Цель статьи
Будут рассмотрены основные элементы, такие как символы, операторы, выноски и индексы, а также способы их использования и оформления с помощью соответствующих тегов HTML.
После прочтения этой статьи вы сможете создавать формулы в HTML без ошибок и сможете правильно оформить основные элементы формулы, чтобы привлечь внимание читателя и улучшить восприятие информации.
Независимо от ваших познаний в HTML и математике, данная статья поможет вам разобраться с основами создания формул в HTML и использованием соответствующих тегов для их оформления.
Видео:Как строить структурные формулы быстро, как ФЛЭШ — Мое полное РуководствоСкачать

Обзор содержания
В статье рассматривается структура формулы и ее основные элементы. В первой части объясняется, что такое формула и для чего она нужна. Рассматриваются различные виды формул и их применение в разных областях знания.
Далее идет описание основных элементов формулы, таких как переменные, операторы, функции и константы. Объясняется, какие значения могут принимать переменные и какие операторы используются для их обработки. Также рассматриваются функции и их роль в формулах.
Особое внимание уделяется правилам написания формулы. Описывается синтаксис формулы и правила приоритета операторов. Объясняется, как правильно расставлять скобки и какие ошибки допускаются при написании формулы.
В заключительной части статьи приводятся примеры использования формул. Показывается, как можно применить формулы для решения различных задач: от математических вычислений до анализа данных и моделирования процессов.
Все эти знания помогут вам лучше понять структуру формулы и использовать ее в своей работе. Вы научитесь правильно составлять формулы и извлекать нужную информацию из них. Это важный навык, который пригодится во многих областях деятельности.
Понятие структуры формулы
Ключевыми элементами структуры формулы являются:
- Переменные: символы, которые представляют неизвестные или изменяющиеся значения в выражении. Они обозначаются латинскими буквами.
- Операции: действия, выполняемые над переменными для получения результата. Операции могут быть арифметическими (+, -, *, /), логическими (>, <, =) или другого типа.
- Функции: специальные операции, которые принимают одно или более значений в качестве аргументов и возвращают результат. Например, функция СУММА возвращает сумму заданных чисел.
- Скобки: используются для указания порядка выполнения операций и группировки частей формулы. Скобки могут быть круглыми ( ), квадратными [ ] или фигурными { }.
Правильная структура формулы гарантирует правильность расчета и позволяет избежать двусмысленности или неправильного толкования выражения. При составлении формулы необходимо следить за последовательностью операций и правильным использованием переменных, функций и скобок.
Например, формула для вычисления площади прямоугольника может выглядеть так: S = a * b, где S — площадь, а и b — длины сторон прямоугольника. В этом случае, структура формулы определяет порядок вычислений и связь между переменными.
Таким образом, понимание структуры формулы является важным элементом для правильного использования математических выражений и получения верных результатов.
Примеры структуры формулы
Ниже приведены несколько примеров структуры формулы:
Пример 1:
Формула для вычисления площади прямоугольника: S = a * b, где a и b — длины сторон прямоугольника.
Пример 2:
Формула для вычисления объема цилиндра: V = π * r2 * h, где π — число пи, r — радиус основания цилиндра, h — высота цилиндра.
Пример 3:
Формула для вычисления суммы арифметической прогрессии: S = (n / 2) * (2a + (n — 1)d), где n — количество элементов прогрессии, a — первый элемент, d — разность прогрессии.
Это лишь несколько примеров, и в реальных математических и научных областях могут использоваться более сложные формулы и структуры.
Значение основных элементов
Аргументы: Аргументы представляют значения или переменные, которые передаются функции для выполнения операций. Аргументы могут быть числами, текстом или ссылками на ячейки в таблице.
Операторы: Операторы используются для комбинирования аргументов и выполнения различных операций. Операторы могут быть арифметическими, логическими или сравнениями.
Ссылки на ячейки: Ссылки на ячейки позволяют обращаться к данным, содержащимся в определенных ячейках таблицы. Ссылки на ячейки обеспечивают гибкость и возможность обновления формулы при изменении данных.
Форматирование: Форматирование элементов формулы влияет на их отображение и понимание. Некоторые элементы могут быть выделены жирным шрифтом для обозначения важности, а другие могут быть курсивом для выделения терминов или значений.
Итоговое значение: Итоговое значение формулы отображает результат выполнения операций и функций. Это значение может быть числом, текстом или значением ошибки, если формула содержит некорректные данные или операции.
Важно точно прописывать каждый из основных элементов в формуле, чтобы достичь желаемого результата и избежать ошибок в расчетах.
Видео:СТРОЕНИЕ АТОМА ХИМИЯ 8 класс // Подготовка к ЕГЭ по Химии - INTENSIVСкачать

Состав структуры формулы
1. Переменные. Переменные являются основными элементами формулы. Они представляют собой символы, обозначающие неизвестные или изменяющиеся величины, которые могут принимать различные значения. Обычно переменные обозначаются буквами латинского алфавита, например, x, y, z.
2. Операции. Операции выполняют различные математические действия над переменными или другими элементами формулы. Наиболее распространенные операции включают сложение, вычитание, умножение и деление.
3. Константы. Константы — это фиксированные значения, которые остаются неизменными в течение всего вычисления. Например, число π (пи) является константой и обозначается символом π.
4. Скобки. Скобки используются для группировки элементов формулы и управления порядком выполнения операций. Наиболее часто встречаются круглые скобки, но также могут использоваться квадратные и фигурные скобки.
5. Функции. Функции позволяют применять математические операции к переменным или другим элементам формулы. Примеры функций включают синус, косинус, экспоненту и логарифм.
6. Знаки равенства и неравенства. Знаки равенства (=) и неравенства (≠, <, >) используются для сравнения величин и установления соотношений между ними.
Комбинируя эти основные элементы, мы можем создавать сложные формулы, которые описывают различные математические концепции и явления.
Элементы и их роль
Структура формулы основана на нескольких элементах, каждый из которых играет свою роль в обозначении математических выражений и операций. Вот некоторые основные элементы, используемые в формулах:
| Элемент | Роль |
|---|---|
| Параметры | Параметры представляют собой переменные или константы, которые используются в формулах для представления различных значений. Они могут быть обозначены буквами или символами и представлять числа или другие значения. |
| Операторы | Операторы являются символами или командами, которые выполняют различные операции, такие как сложение, вычитание, умножение и деление. Они используются для объединения параметров и других элементов, чтобы выполнить определенные вычисления. |
| Функции | Функции — это специальные математические операции, которые могут быть применены к одному или нескольким параметрам, чтобы получить результат. Функции могут быть предопределены или пользовательские и выполнять различные операции, такие как вычисление синуса или квадратного корня. |
| Скобки | Скобки используются для управления порядком выполнения операций и группировки элементов в формуле. Они могут использоваться для указания приоритета операций и изменения смысла выражений. |
Эти элементы образуют основу формул и позволяют создавать сложные математические выражения для решения различных задач. Понимание и использование этих элементов является важной частью математической грамотности и позволяет четко и точно выражать математические идеи и концепции.
Взаимосвязь элементов
Структура формулы математического выражения или химического состава имеет определенную взаимосвязь между своими элементами. Под элементами понимаются числа, переменные, операции и другие символы, которые используются в формуле.
Числа являются основными элементами формулы и обозначают определенное количество или значение. Они могут быть целыми или дробными числами, положительными или отрицательными.
Переменные представляют собой обозначения величин или неизвестных значений, которые могут быть заменены на конкретные числа или значения. Они обычно обозначаются буквами и могут использоваться для представления различных физических, химических или математических величин.
Операции используются для выполнения математических действий над числами или переменными. Они могут быть арифметическими (сложение, вычитание, умножение, деление), алгебраическими (возведение в степень, извлечение корня) или логическими (логическое умножение, логическое сложение).
Символы и знаки используются для обозначения различных математических функций, операций или отношений. Например, символ «π» используется для обозначения числа «пи», символ «√» используется для обозначения извлечения квадратного корня.
Элементы формулы связаны друг с другом в определенном порядке, и их взаимосвязь определяет значение и смысл всей формулы. Например, в математическом выражении «2 + 3 * 4», операция умножения имеет более высокий приоритет, чем операция сложения, поэтому сначала выполняется умножение, а затем сложение. Это позволяет получить правильный результат вычисления.
Изучение взаимосвязи элементов формулы позволяет понять ее структуру и правильно интерпретировать ее значение. Это особенно важно при работе с сложными математическими или химическими формулами, где неверное понимание взаимосвязи элементов может привести к ошибкам и неправильным результатам.
Видео:Строение атома. Как составить электронную и электронно-графическую формулы?Скачать

Применение структуры формулы
Одним из основных применений структуры формулы является ее использование в уравнениях. Уравнение – это математическое выражение, в котором присутствуют неизвестные переменные, которые нужно найти. С помощью структуры формулы можно записать уравнение в удобной форме, указывая все входящие в него элементы и их связи.
Кроме того, структура формулы позволяет удобно записывать и анализировать различные физические законы и формулы. Например, закон сохранения энергии или закон Ома можно представить в виде уравнений, в которых присутствуют различные символы и операции.
Структура формулы также широко применяется в химии для записи химических реакций. С помощью формулы можно указать состав веществ, их стехиометрию и другие химические параметры.
В области информатики и программирования структура формулы используется для представления алгоритмов и логических выражений. Она позволяет описать последовательность действий и связи между ними в виде логических выражений.
Таким образом, структура формулы имеет широкое применение в различных научных и технических областях. Она позволяет удобно записывать и анализировать сложные математические и физические соотношения, а также представлять их в удобной и понятной форме.
Роль в математике
Формулы помогают математикам исследовать и анализировать различные явления и связи в науке, физике, экономике и других областях. Они облегчают решение задач и проведение вычислений, позволяя сократить и упростить выражения. Формулы также играют важную роль в образовании, помогая студентам изучать и понимать различные математические концепции и теории.
В математике существует множество различных типов формул, включая алгебраические, геометрические, статистические и тригонометрические формулы. Каждый тип формулы имеет свой собственный набор символов, операций и правил, которые позволяют работать с ними.
Использование формулы требует точности и внимательности, поскольку даже малейшая ошибка в записи или операции может привести к неверному результату. Поэтому умение правильно составлять и применять формулы является неотъемлемой частью математической грамотности.
Применение в физике
Формулы в физике используются для решения задач и вычислений в различных областях этой науки. Они позволяют определить величины, связанные с движением, энергией, силой, взаимодействием частиц и другими физическими величинами.
Например, закон Ньютона о движении может быть выражен с помощью формулы F = ma, где F — сила, m — масса объекта, a — ускорение. Эта формула позволяет ученым определить силу, действующую на объект, и его ускорение.
Другой пример — формула Герца, используемая для расчета частоты электромагнитной волны. Эта формула связывает частоту f с длиной волны λ и скоростью света c: f = c/λ. Она позволяет определить частоту электромагнитной волны на основе ее длины волны и наоборот.
Таким образом, формулы играют важную роль в физике, позволяя ученым анализировать, прогнозировать и описывать различные физические явления и процессы.
Использование в химии
В химических формулах элементы обозначаются символами, при этом капитализация символа играет большую роль, так как она указывает на различные свойства элемента. Например, символ «H» обозначает элемент водород, а символ «He» обозначает гелий.
Формулы также позволяют указать количество атомов каждого элемента в молекуле. Например, формула воды H2O указывает на то, что в одной молекуле воды содержится 2 атома водорода и 1 атом кислорода.
Химические реакции также записываются с использованием формул. Например, реакция горения метана CH4 представляется следующим образом: CH4 + 2O2 = CO2 + 2H2O. Эта формула показывает, что при горении метана образуется углекислый газ и вода.
Формулы также могут использоваться для обозначения химических связей между атомами в молекуле. Например, формула этилового спирта C2H5OH показывает, что в молекуле этилового спирта присутствуют атомы углерода, водорода и кислорода, а также показывает, как они связаны друг с другом.
📽️ Видео
Компоненты крови - из чего состоит кровь? Эритроциты, лейкоциты, плазма и дрСкачать

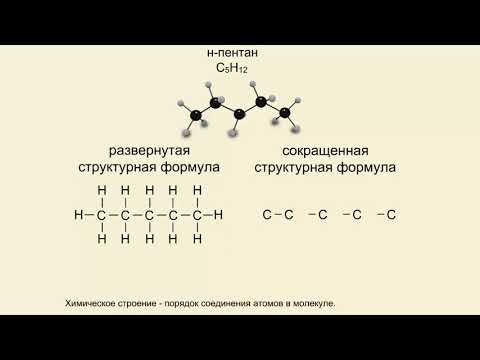
Строение органических соединений. Структурные формулыСкачать
КАК ДАВАТЬ НАЗВАНИЯ органическим соединениям | КАК СОСТАВЛЯТЬ ФОРМУЛЫ в органической химииСкачать

Строение клетки за 8 минут (даже меньше)Скачать

Строение и функции белков.Скачать

8 класс. Распределение электронов в атоме. Электронные формулы.Скачать

Егэ Химия 🧪 структурная формула.Скачать

Состав и структура органических веществ. Изомерия. 1 часть. 10 класс.Скачать

Видео №3. Как составить изомерыСкачать

Электронные конфигурации атомов. Химия – простоСкачать

СОЛИ ХИМИЯ 8 КЛАСС // Урок Химии 8 класс: Классификация солей, Формулы Солей, Кислотный ОстатокСкачать

Основные фонды Понятие и классификация основных фондовСкачать

БЕЗ ЭТОГО НЕ СДАТЬ ЕГЭ по Химии — Электронная конфигурация атомаСкачать

Логические выражения, таблицы истинности ,структурная логическая схемаСкачать

Жизненная химия | структурные формулыСкачать
