Смешанное произведение векторов — важное понятие в векторной алгебре, которое играет значительную роль в геометрической теории и физике. Смешанное произведение позволяет описывать свойства трехмерных объектов и вычислять их объемы, площади, и другие характеристики.
Смешанное произведение векторов определяется как скалярное произведение вектора и векторного произведения двух других векторов. Формула для вычисления смешанного произведения векторов ABC и ABD может быть записана следующим образом:
(ABC, ABD) = ABC · (AB × AC)
Где:
- ABC, ABD — векторы, для которых вычисляется смешанное произведение;
- AB, AC, AD — векторы, используемые для вычисления векторного произведения;
- · — скалярное произведение;
- × — векторное произведение.
Смешанное произведение векторов обладает рядом важных свойств, которые делают его полезным в различных областях науки и техники. Например, смешанное произведение может быть использовано для вычисления объема параллелепипеда, образованного тремя векторами. Также, смешанное произведение векторов позволяет определять, лежат ли три точки на одной плоскости или нет.
Знание и понимание смешанного произведения векторов являются неотъемлемой частью изучения векторной алгебры и геометрии. Понимая его определение и свойства, можно решать разнообразные задачи, связанные с геометрией и физикой, и получать более полное представление о трехмерном пространстве.
Видео:Аналитическая геометрия, 4 урок, Смешанное произведениеСкачать

Смешанное произведение векторов
Определение смешанного произведения векторов определяется следующим образом. Пусть a, b и c — это три вектора, заданные в пространстве. Тогда смешанное произведение векторов определяется как скалярное произведение между вектором a и векторным произведением векторов b и c.
Математическая запись смешанного произведения векторов выглядит следующим образом: a∙(b×c). Здесь × обозначает векторное произведение между векторами b и c.
Смешанное произведение векторов имеет несколько свойств, которые следует учитывать. Например, оно является антисимметричной функцией, что означает, что a∙(b×c) = -b∙(a×c). Оно также удовлетворяет правилу распределительности относительно сложения двух векторов.
| Свойства смешанного произведения векторов |
|---|
| a∙(b×c) = b∙(c×a) = c∙(a×b) |
| a∙(b×c) = -b∙(a×c) |
| a∙(b+c) = a∙b + a∙c |
Смешанное произведение векторов имеет геометрическую интерпретацию. Оно равно объему параллелепипеда, построенного на трех векторах a, b и c. Если векторы a, b и c образуют правую тройку, то смешанное произведение положительно. Если они образуют левую тройку, то смешанное произведение отрицательно.
Смешанное произведение векторов связано с скалярным и векторным произведением. В частности, его можно выразить через эти операции следующим образом: a∙(b×c) = (a∙b)c — (a∙c)b. Это свойство позволяет использовать смешанное произведение для вычисления других векторных операций.
Видео:Смешанное произведение векторовСкачать

Определение
Смешанное произведение векторов определяется следующим образом: для векторов a, b и c смешанное произведение равно скалярному произведению вектора a на векторное произведение векторов b и c.
Математически это можно записать так:
(a · (b × c))
где · — скалярное произведение векторов, × — векторное произведение векторов.
Что такое смешанное произведение векторов?
Смешанное произведение векторов можно представить геометрически. Предположим, у нас есть три вектора a, b и c. Смешанное произведение векторов определяется как объем параллелепипеда, образованного этими векторами.
Геометрическая интерпретация смешанного произведения векторов позволяет нам понять его свойства и значения. Например, если смешанное произведение векторов равно нулю, это означает, что векторы a, b и c лежат в одной плоскости. Если же смешанное произведение векторов положительно, то векторы a, b и c образуют правую тройку векторов, а если отрицательно — то левую.
Смешанное произведение векторов также обладает рядом важных свойств. Оно является линейной операцией, то есть для любых векторов a, b и c и любого числа k справедливо равенство: смешанное произведение (ka, b, c) = k(а, b, c).
Смешанное произведение векторов имеет связь с скалярным и векторным произведением. Например, смешанное произведение векторов (a, b, с) можно выразить через скалярное и векторное произведения следующим образом: (a, b, c) = a · (b x c), где x — операция векторного произведения.
Свойства смешанного произведения векторов позволяют его использовать в различных областях науки и техники. Оно находит применение в физике, геометрии, механике, электротехнике и других дисциплинах. Благодаря своей геометрической интерпретации и свойствам, смешанное произведение векторов является мощным и универсальным инструментом для решения различных задач и построения математических моделей.
Геометрическая интерпретация
Геометрическая интерпретация смешанного произведения векторов в пространстве заключается в том, что это объем параллелепипеда, построенного на векторах.
Пусть у нас есть три вектора a, b и c. Тогда смешанное произведение этих векторов можно рассматривать как объем параллелепипеда, построенного на этих трех векторах. Ориентация этого параллелепипеда зависит от порядка векторов: если поменять местами вектора, то и ориентация параллелепипеда изменится.
Геометрическая интерпретация смешанного произведения векторов позволяет понять, что значение смешанного произведения равно нулю тогда и только тогда, когда эти вектора лежат в одной плоскости. Если же векторы не лежат в одной плоскости, то объем параллелепипеда, построенного на них, будет отличен от нуля.
Геометрическая интерпретация позволяет говорить о смешанном произведении векторов как о векторе, т.к. его направление и длина также имеют смысл в геометрической интерпретации.
Таким образом, геометрическая интерпретация смешанного произведения векторов позволяет увидеть связь между смешанным, скалярным и векторным произведениями векторов, а также обобщить понятие объема трехмерной фигуры на произвольные векторы в трехмерном пространстве.
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Свойства
Смешанное произведение векторов обладает несколькими важными свойствами, которые помогают понять его физическую и геометрическую интерпретацию.
Первое свойство — ассоциативность. Для любых трех векторов a, b и c смешанное произведение удовлетворяет следующему равенству:
(a × b) ♦ c = a ♦ (b × c)
То есть порядок векторов не влияет на результат смешанного произведения.
Второе свойство — линейность. Смешанное произведение линейно по каждому из трех векторов.
Для любых векторов a, b и c, а также скаляра k, справедливы следующие равенства:
(ka) ♦ b = k(a ♦ b)
a ♦ (kb) = k(a ♦ b)
(a + b) ♦ c = a ♦ c + b ♦ c
a ♦ (b + c) = a ♦ b + a ♦ c
Третье свойство — невырожденность. Смешанное произведение равно нулю тогда и только тогда, когда все три вектора коллинеарны, то есть находятся на одной прямой или в плоскости.
Четвертое свойство — соотношение с скалярным и векторным произведением. Смешанное произведение может быть выражено через скалярное и векторное произведения следующим образом:
a ♦ (b × c) = a · (b × c) = (a × b) · c
Эти свойства помогают в использовании смешанного произведения в различных задачах, связанных с векторами и геометрией.
Связь со скалярным и векторным произведением
Смешанное произведение векторов имеет тесную связь со скалярным и векторным произведением.
- Смешанное произведение векторов можно выразить через скалярное и векторное произведение. Пусть у нас есть три вектора a, b и c. Тогда смешанное произведение векторов можно выразить следующим образом: a · (b × c). Здесь a — скалярное произведение векторов a и (b × c), которое определяется как произведение модулей этих векторов и косинуса угла между ними.
- Геометрически интерпретируя, смешанное произведение векторов представляет собой объем параллелепипеда, построенного на векторах a, b и c. Знак этого смешанного произведения определяется правой системой координат: если результат положителен, это означает, что векторы a, b и c ориентированы в правую сторону относительно нашей системы координат, если отрицателен — они ориентированы в левую сторону.
Таким образом, смешанное произведение векторов связывает скалярное и векторное произведение и имеет геометрическую интерпретацию в виде объема параллелепипеда.
Свойства смешанного произведения
Смешанное произведение векторов обладает рядом свойств, которые делают его полезным и удобным инструментом при решении различных задач. Вот некоторые из наиболее важных свойств:
- Смешанное произведение векторов не зависит от выбора начала координат. Это означает, что результат смешанного произведения будет одинаковым, независимо от того, в какой системе координат оно рассчитывается.
- Смешанное произведение векторов обращается в ноль, если все векторы лежат в одной плоскости. Это свойство позволяет определить, лежат ли векторы в одной плоскости или нет.
- Значение смешанного произведения векторов имеет смысл объема параллелепипеда, построенного на этих векторах. Таким образом, смешанное произведение может быть использовано для вычисления объема трехмерных фигур.
- Смешанное произведение обладает свойством аддитивности. Это значит, что смешанное произведение суммы векторов равно сумме смешанных произведений этих векторов.
- Если один из векторов в смешанном произведении равен нулю, то и всё смешанное произведение будет равно нулю.
- Смешанное произведение векторов меняет знак при изменении порядка векторов. То есть, если поменять местами два вектора, то знак смешанного произведения также поменяется.
Эти свойства делают смешанное произведение векторов мощным инструментом для работы с трехмерной геометрией и решения различных физических задач. Оно позволяет определить объемы трехмерных фигур, проверить, лежат ли векторы в одной плоскости, а также выполнять другие вычисления, связанные с трехмерными векторами.
🌟 Видео
Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

Скалярное произведение векторов. 9 класс.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

А.7.10 Смешанное произведение векторовСкачать

§18 Свойства смешанного произведенияСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

Смешанное произведение трех векторов, свойстваСкачать

§17 Смешанное произведение векторовСкачать

Математика без Ху!ни. Свойства скалярного и векторного произведений.Скачать

Векторное произведение векторовСкачать

Лекция 19. Векторное произведение векторов и его свойства.Скачать

9 класс, 20 урок, Свойства скалярного произведения векторовСкачать

Векторное произведение векторов | Высшая математикаСкачать

Лекция 21. Смешанное произведение векторов и его свойства.Скачать

Аналитическая геометрия, 3 урок, Векторное произведениеСкачать

Смешанное произведениеСкачать
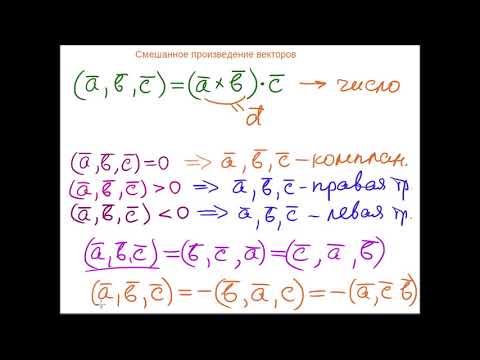
Смешанное произведение векторовСкачать
