Диагональ — это одна из наиболее важных характеристик треугольника. Она является отрезком, соединяющим два его вершины, не являющихся соседними.
Найти длину диагонали в треугольнике может показаться сложной задачей, особенно для тех, кто не обладает математическим образованием. Однако, с помощью некоторых элементарных формул и методов, вы сможете легко и быстро решить эту задачу.
Существуют различные способы определения длины диагонали в треугольнике, но самый распространенный и простой — использование теоремы Пифагора. Согласно этой теореме, длина диагонали треугольника может быть определена с помощью известной длины его сторон.
В этом практическом руководстве мы рассмотрим шаг за шагом процесс нахождения длины диагонали в треугольнике с помощью теоремы Пифагора, а также предоставим примеры, которые помогут вам лучше понять материал.
- Метод 1: По формуле Пифагора
- Определение длин сторон треугольника
- Применение формулы Пифагора для нахождения длины диагонали
- Метод 2: Использование закона синусов
- Измерение углов треугольника
- Вычисление длин сторон треугольника с помощью логических операций
- Метод 3: Использование закона косинусов
- Определение длин сторон треугольника
- Вычисление длины диагонали с использованием закона косинусов
- 🔍 Видео
Видео:Как найти диагональ... Диагональни топишСкачать

Метод 1: По формуле Пифагора
Формула Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Применение формулы Пифагора к не прямоугольному треугольнику основано на теореме о косинусах. В треугольнике ABC диагональ AC является гипотенузой, а стороны AB и BC – катетами. Таким образом, имеем:
- AB2 + BC2 = AC2
Чтобы найти длину диагонали AC, нужно подставить значения известных сторон AB и BC в формулу Пифагора и вычислить результат.
Определение длин сторон треугольника
Для определения длин сторон треугольника необходимо провести измерения и использовать геометрические формулы.
При наличии данных о координатах вершин треугольника можно использовать формулы расстояния между точками для определения длин сторон. Например, можно воспользоваться формулой расстояния между двумя точками в декартовой системе координат:
Для двух точек A(x1, y1) и B(x2, y2) расстояние между ними равно:
AB = √((x2 — x1)^2 + (y2 — y1)^2)
Применяя данную формулу к каждой паре вершин треугольника, можно определить длины всех его сторон.
Если известны углы треугольника и длина одной из его сторон, можно воспользоваться тригонометрическими функциями для определения длин остальных сторон. Например, для треугольника ABC, где AB — известная сторона, а α и β — углы, можно использовать формулы:
BC = AB * sin(α) / sin(β)
AC = AB * sin(β) / sin(α)
Применяя данные формулы к известной стороне и углам треугольника, можно вычислить длины остальных его сторон.
Таким образом, с помощью формул расстояния между точками и тригонометрических функций, можно определить длины сторон треугольника и использовать их для решения различных задач, включая нахождение длины диагонали и других величин.
| Первая вершина | Вторая вершина | Длина стороны |
|---|---|---|
| A | B | AB |
| B | C | BC |
| C | A | AC |
Применение формулы Пифагора для нахождения длины диагонали
Формула Пифагора также известна как теорема Пифагора и гласит:
a2 + b2 = c2,
где a и b — длины катетов треугольника, а c — длина гипотенузы, которая является диагональю треугольника.
Чтобы найти длину диагонали треугольника, необходимо знать длины двух сторон треугольника, которые образуют прямой угол.
Для использования формулы Пифагора следует выполнить следующие шаги:
- Определите длины сторон треугольника, образующих прямой угол.
- Возвести в квадрат длины этих сторон.
- Сложите полученные значения.
- Вычислите квадратный корень полученной суммы.
После выполнения этих шагов вы получите длину диагонали треугольника.
Применение формулы Пифагора позволяет находить не только длину диагонали прямоугольного треугольника, но и выполнять другие вычисления, связанные с геометрией.
Видео:как найти диагональ.Скачать
Метод 2: Использование закона синусов
Чтобы найти длину диагонали в треугольнике, мы можем использовать закон синусов. Закон синусов утверждает, что отношение длины стороны треугольника к синусу противолежащего ей угла равно одинаково для всех сторон и их противолежащих углов.
Для нахождения диагонали треугольника сначала нам необходимо найти два измерения: длину одной из сторон треугольника и меру одного из противолежащих углов. Затем мы можем использовать закон синусов, который имеет следующий вид:
- Делаем противолежащую сторону равной «a».
- Делаем противолежащий угол равным «A».
- Делаем сторону, смежную с углом «A», равной «b».
- Делаем угол, смежный с стороной «b», равным «B».
- Делаем диагональ треугольника равной «c».
- Тогда закон синусов можно записать в виде формулы:
$$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$$
Используя данную формулу, мы можем найти длину диагонали треугольника, если известны длина одной из сторон и мера одного из углов.
Применение закона синусов может быть полезным, когда нужно найти длину диагонали в треугольнике без измерения самой диагонали. Этот метод особенно эффективен, когда нам известны длины сторон и углы треугольника.
Измерение углов треугольника
Размер углов в треугольнике играет важную роль при вычислении его диагонали. Углы треугольника могут быть измерены с помощью различных инструментов и методов.
Самый простой способ измерения углов — использование геодезического инструмента, такого как транспортир или гониометр. Эти инструменты позволяют вам точно измерить углы между сторонами треугольника.
Если у вас нет геодезического инструмента, вы можете использовать геометрические формулы и теоремы для определения углов треугольника. Например, теорема синусов позволяет найти углы треугольника, зная длины его сторон.
Для измерения углов можно также использовать тригонометрические функции, такие как синус, косинус и тангенс. Для этого необходимо знать длины сторон треугольника и использовать тригонометрические формулы для вычисления углов.
Измерение углов треугольника является важным шагом при вычислении его длины диагонали. Точное измерение углов поможет вам получить более точный результат при вычислении диагонали треугольника.
Важно помнить: при измерении углов треугольника необходимо быть аккуратным и точным. Даже небольшая погрешность при измерении может привести к неточному результату при вычислении диагонали треугольника.
Вычисление длин сторон треугольника с помощью логических операций
Для вычисления длин сторон треугольника с помощью логических операций необходимо знать длины двух других сторон треугольника и угол между ними. Кроме того, требуется знание геометрических формул для вычисления длины третьей стороны треугольника.
Прежде чем приступить к вычислению длин сторон треугольника, необходимо убедиться, что заданные значения удовлетворяют неравенству треугольника. Треугольник существует только, если сумма длин любых двух его сторон больше длины третьей стороны.
Если значения сторон удовлетворяют неравенству треугольника, можно приступить к вычислению длины третьей стороны с помощью логических операций.
Для вычисления длины третьей стороны треугольника можно использовать формулу:
a^2 + b^2 = c^2
где a и b — длины двух сторон, а c — искомая длина третьей стороны.
Для расчета длины третьей стороны треугольника с помощью логических операций используются следующие шаги:
- Возведение в квадрат длин двух известных сторон треугольника.
- Сложение результатов возведения в квадрат.
- Вычисление квадратного корня из полученной суммы.
Таким образом, при наличии длин двух сторон треугольника и угла между ними, можно вычислить длину третьей стороны с помощью логических операций. Данная информация особенно полезна при решении задач, связанных с геометрией и треугольниками.
Видео:Диагональ прямоугольника. Математика. Геометрия.Скачать

Метод 3: Использование закона косинусов
Если в треугольнике известны длины всех трех сторон, можно использовать закон косинусов для вычисления длины диагонали. Закон косинусов утверждает, что квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон, умноженных на косинус соответствующего угла.
Для вычисления длины диагонали можно использовать следующую формулу:
c^2 = a^2 + b^2 — 2abcosC
Где:
- c — длина диагонали
- a, b — длины сторон треугольника
- C — угол, противолежащий диагонали
Используя данную формулу, можно рассчитать длину диагонали треугольника, если известны длины его сторон и углы.
Определение длин сторон треугольника
Существует несколько способов определить длины сторон треугольника:
| 1. Используя формулу длины стороны по координатам вершин: | ab = sqrt((x2 — x1)^2 + (y2 — y1)^2) |
| 2. Известными длинами других сторон и углов: | a = c * sin(A) / sin(C) |
| 3. Используя теорему Пифагора: | a = sqrt(b^2 + c^2 — 2 * b * c * cos(A)) |
Выбор метода определения длины сторон треугольника зависит от доступных данных и условий задачи. В каждом методе необходимо использовать известные величины, такие как координаты вершин, длины других сторон или углы.
После определения длин сторон треугольника можно приступать к вычислению длины его диагонали, следуя дальнейшим указаниям.
Вычисление длины диагонали с использованием закона косинусов
Для вычисления длины диагонали треугольника можно использовать закон косинусов. Этот закон позволяет найти длину одной из сторон треугольника, если известны длины двух других сторон и угол между ними.
Формула для вычисления длины диагонали с использованием закона косинусов выглядит следующим образом:
c^2 = a^2 + b^2 — 2ab * cos(C)
Где:
- c — длина диагонали
- a и b — длины сторон треугольника
- C — угол между сторонами a и b
Чтобы вычислить длину диагонали, необходимо знать значения a, b и C. После подстановки этих значений в формулу, выполните соответствующие вычисления и получите результат.
Использование закона косинусов позволяет найти длину диагонали треугольника в случаях, когда известны его стороны и углы. Это удобный и эффективный способ решения задачи нахождения длины диагонали в треугольнике.
🔍 Видео
Хитрости в решении геометрических задач в ОГЭ по математике | Математика TutorOnlineСкачать

10 класс, 24 урок, Прямоугольный параллелепипедСкачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Найти диагональ квадратаСкачать
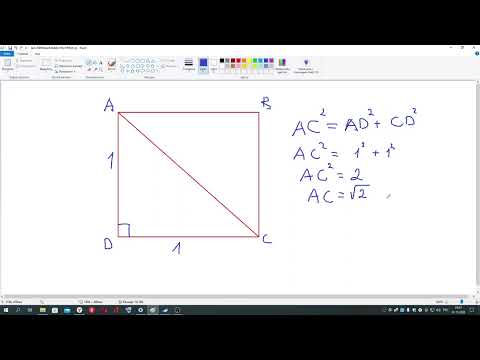
КАК РАЗМЕТИТЬ ФУНДАМЕНТ СВОИМИ РУКАМИ / КАК НАЙТИ ДИАГОНАЛИ ФУНДАМЕНТА / КАК ВЫСТАВИТЬ ПРЯМОЙ УГОЛ /Скачать

17 задание из ОГЭ. Найти диагональ квадратаСкачать

Диагональ прямоугольника образует угол 50° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Как вычислить диагональ прямоугольника. Для начинающих сварщиковСкачать

Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Диагональ многоугольникаСкачать

8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

как найти высоту крыши и длину стропило по углу наклонаСкачать

8 класс, 7 урок, ПрямоугольникСкачать

ПРАВИЛЬНАЯ диагональ! Самый простой и точный способ.Разметка фундаментаСкачать

Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

Периметр прямоугольника. Как найти периметр прямоугольника?Скачать
