Дробные числа — это неотъемлемая часть математики и нашей повседневной жизни. В процессе работы с дробями возникают различные вопросы, из которых один из наиболее частых — можно ли сокращать дроби при сложении и вычитании? В данной статье мы разберем этот вопрос и дадим полное объяснение.
Для начала, давайте разберемся, что такое сокращение дробей. Сокращение дроби означает упрощение ее записи путем деления числителя и знаменателя на их общий делитель. Таким образом, сократив дробь, мы получаем эквивалентную ей дробь с меньшими числителем и знаменателем.
Ответ на вопрос о возможности сокращения дробей при сложении и вычитании зависит от конкретной задачи. Если мы складываем или вычитаем дроби с одинаковыми знаменателями, то да, мы можем сократить полученную дробь. Однако, если знаменатели разные, то сокращение дробей невозможно.
Важно понимать, что при сложении и вычитании дробей с разными знаменателями необходимо привести дроби к общему знаменателю. После этого мы можем складывать или вычитать числители, сохраняя знаменатель неизменным. Таким образом, результатом сложения или вычитания будет дробь с тем же знаменателем, что и исходные дроби.
- Что такое дроби
- Определение дроби
- Примеры дробей
- Пример 1:
- Пример 2:
- Дроби в сложении и вычитании
- Общее объяснение
- Примеры сложения и вычитания дробей
- Понятие сокращенных дробей
- Что такое сокращенные дроби
- Определение сокращения дроби
- Примеры сокращенных дробей
- Как сокращать дроби
- Методы сокращения дробей
- Правила сокращения дробей
- Сокращение дробей при сложении и вычитании
- Возможно ли сокращать дроби
- Разные точки зрения
- Математические принципы
- Примеры сокращения дробей при сложении и вычитании
- Конкретные числовые примеры
- Подробный анализ сокращения
- 📺 Видео
Видео:Основное свойство дроби. Сокращение дробей. 5 класс.Скачать

Что такое дроби
Числитель – это число, которое показывает, сколько частей целого числа мы рассматриваем. Знаменатель – это число, которое показывает, на сколько частей мы делим целое число.
Например, дробь 3/4 означает, что мы рассматриваем 3 части из 4 возможных.
Дроби обычно используются для представления нецелых чисел и десятичных дробей. Они могут быть положительными или отрицательными.
В математике дроби могут быть сложены или вычтены друг из друга. При сложении и вычитании дробей важно привести их к общему знаменателю. Это позволяет производить операции с числителями и получить итоговую дробь с сокращенными числителем и знаменателем при необходимости.
Например, при сложении дробей 3/4 и 1/2 мы приводим их к общему знаменателю, в данном случае это 4. Получаем: (3/4) + (1/2) = (6/8) + (4/8) = 10/8, что можно упростить до 5/4.
Таким образом, сокращение дробей возможно при сложении и вычитании, и оно позволяет получить более простую или удобочитаемую форму дробей.
Определение дроби
Обозначение дроби выглядит как a/b, где a – числитель, а b – знаменатель. Числитель и знаменатель могут быть любыми целыми числами.
Например, дробь 3/4 можно прочитать как «три четверти» или «три четвертых». В данном случае числитель равен 3, а знаменатель равен 4. Это означает, что мы берем три одинаковых части, каждая из которых составляет часть от целого, разделенной на четыре равные части.
Дроби используются для представления частей целых чисел, нецелых чисел и десятичных дробей. Они могут быть положительными или отрицательными. Дроби широко применяются в математике, науке, финансах, инженерии и других областях.
| Термин | Определение |
|---|---|
| Числитель | Число, находящееся над чертой дроби. |
| Знаменатель | Число, находящееся под чертой дроби. |
| Десятичная дробь | Дробь, в которой знаменатель – 10 в некоторой степени. |
| Нецелое число | Число, представленное дробью. |
| Целое число | Число, которое не является дробью. |
Примеры дробей
Пример 1:
Пусть имеем дроби 3/4 и 2/5. Чтобы сложить эти дроби, необходимо привести их к общему знаменателю. В данном случае общий знаменатель будет равен 20.
Теперь проведем сложение: 3/4 + 2/5 = 15/20 + 8/20 = 23/20.
Итак, результатом сложения дробей 3/4 и 2/5 является дробь 23/20.
Пример 2:
Рассмотрим дроби 7/8 и 3/4. Для вычитания также необходимо привести дроби к общему знаменателю. В данном случае общим знаменателем является 8.
Вычитание будет выглядеть следующим образом: 7/8 — 3/4 = 7/8 — 6/8 = 1/8.
Таким образом, разностью между дробями 7/8 и 3/4 будет дробь 1/8.
Это лишь несколько примеров использования дробей при сложении и вычитании. В каждом случае необходимо привести дроби к общему знаменателю и выполнить требуемую операцию. При этом, сокращать дроби необязательно, так как результат может быть представлен в несократимой форме.
Видео:Как можно и нельзя сокращать дробиСкачать

Дроби в сложении и вычитании
При сложении и вычитании дробей, важно понимать, что для выполнения этих операций необходимо привести дроби к общему знаменателю. Как правило, это происходит путем нахождения наименьшего общего кратного (НОК) знаменателей дробей.
Итак, рассмотрим примеры сложения и вычитания дробей:
Пример 1:
Даны две дроби: $\frac{1}{4}$ и $\frac{3}{8}$. Найдем общий знаменатель:
Знаменатели дробей 4 и 8 имеют общий делитель 4. Так как 8 делится на 4 без остатка, то в данном случае наименьшим общим кратным будет само число 8.
Приведем дроби к общему знаменателю:
$\frac{1}{4} = \frac{2}{8}$
$\frac{3}{8}$
Теперь сложим числители дробей и оставим знаменатель без изменений:
$\frac{2}{8} + \frac{3}{8} = \frac{5}{8}$
Итак, полученная сумма дробей равна $\frac{5}{8}$.
Пример 2:
Даны две дроби: $\frac{3}{5}$ и $\frac{1}{3}$. Найдем общий знаменатель:
Знаменатели дробей 5 и 3 не имеют общих делителей, поэтому общим знаменателем будет их произведение: $5 \cdot 3 = 15$.
Приведем дроби к общему знаменателю:
$\frac{3}{5} = \frac{9}{15}$
$\frac{1}{3} = \frac{5}{15}$
Теперь сложим числители дробей и оставим знаменатель без изменений:
$\frac{9}{15} + \frac{5}{15} = \frac{14}{15}$
Итак, полученная сумма дробей равна $\frac{14}{15}$.
Таким образом, чтобы провести сложение или вычитание дробей, необходимо привести их к общему знаменателю и выполнить операции с числителями, сохраняя знаменатель неизменным.
Общее объяснение
Для сокращения дробей необходимо найти наибольший общий делитель числителя и знаменателя. Наибольший общий делитель — это наибольшее число, которое одновременно является делителем числителя и знаменателя.
Чтобы найти наибольший общий делитель, можно использовать различные методы, например, метод простых делителей или алгоритм Евклида. Определив наибольший общий делитель, нужно поделить числитель и знаменатель на него. После этого дробь будет записана в наименьшем возможном виде.
Сокращение дробей имеет большое значение при выполнении операций со сложными выражениями, так как позволяет упростить их и избежать неудобных и сложных числовых значений. Однако, при сокращении дробей нужно быть внимательным и учитывать возможность потери информации. В некоторых случаях, сокращение дробей может привести к искажению результата.
Таким образом, сокращение дробей при сложении и вычитании полезно и применимо, но требует внимательности и осознанности для достижения правильного результата.
Примеры сложения и вычитания дробей
Примеры сложения дробей:
Пример 1:
2/3 + 3/4 = (2 * 4)/(3 * 4) + (3 * 3)/(4 * 3) = 8/12 + 9/12 = (8 + 9)/12 = 17/12
Пример 2:
1/2 + 1/6 = (1 * 6)/(2 * 6) + (1 * 2)/(6 * 2) = 6/12 + 2/12 = 8/12 = 2/3
Примеры вычитания дробей:
Пример 1:
5/6 — 1/3 = (5 * 3)/(6 * 3) — (1 * 2)/(3 * 2) = 15/18 — 2/6 = 15/18 — 6/18 = (15 — 6)/18 = 9/18 = 1/2
Пример 2:
7/8 — 3/4 = (7 * 4)/(8 * 4) — (3 * 2)/(4 * 2) = 28/32 — 6/8 = 28/32 — 24/32 = (28 — 24)/32 = 4/32 = 1/8
В этих примерах обратим внимание, что перед сложением или вычитанием дробей необходимо найти общий знаменатель (знаменатель, на который оба знаменателя дробей делятся без остатка). Затем числители дробей складываются или вычитаются, а знаменатель остается неизменным.
Видео:Сложение дробей. Как складывать дроби?Скачать

Понятие сокращенных дробей
Чтобы сократить дробь необходимо поделить числитель и знаменатель на их наибольший общий делитель (НОД). НОД — это наибольшее число, на которое можно без остатка разделить и числитель, и знаменатель дроби.
Например, рассмотрим дробь 16/24. НОД числителя 16 и знаменателя 24 равен 8. Таким образом, мы можем сократить дробь, поделив числитель и знаменатель на 8. И получим сокращенную дробь 2/3.
Важно отметить, что при сложении и вычитании дробей также рекомендуется сначала сокращать дроби, если это возможно. Это позволяет работать с более простыми и понятными числами и упрощает вычисления.
Однако, при умножении и делении дробей сокращение не является обязательным шагом, так как результат будет таким же, независимо от наличия или отсутствия сокращения.
Видео:Сократить дробь. Пример 08.Скачать

Что такое сокращенные дроби
Для сокращения дроби необходимо найти наибольший общий делитель (НОД) числителя и знаменателя, и поделить оба числа на этот НОД.
Сокращенные дроби имеют преимущества при выполнении математических операций, таких как сложение и вычитание. При сложении или вычитании дробей, сокращенные дроби упрощают вычисления и могут предоставить более понятные результаты.
Например, если мы сложим две дроби: 3/6 и 4/6, то получим 7/6. Поскольку числитель и знаменатель не имеют общих делителей, то эта дробь уже является сокращенной.
Сокращенные дроби также помогают визуально представить дробь в более простой форме. Например, дробь 6/8 можно представить как сокращенную дробь 3/4, что упрощает восприятие и упрощает операции с дробями.
| Дробь | Сокращенная дробь |
|---|---|
| 2/4 | 1/2 |
| 10/15 | 2/3 |
| 8/12 | 2/3 |
Определение сокращения дроби
Делителем числа является любое число, которое делит его без остатка. Когда числитель и знаменатель имеют общие делители, можно сократить дробь, разделив числитель и знаменатель на эти общие делители.
Сокращение дроби упрощает ее запись и делает ее более компактной. Однако, при сложении или вычитании дробей, сокращение необходимо проводить только после выполнения операции, так как это может повлиять на результат.
Чтобы сократить дробь, необходимо найти все общие делители числителя и знаменателя, а затем разделить оба числа на самый большой общий делитель. Общий делитель называется наибольшим, если он является наибольшим числом, которое делит и числитель, и знаменатель без остатка.
Например, если у нас есть дробь 12/36, то можно найти их общие делители: 1, 2, 3, 4, 6 и 12. Наибольший общий делитель равен 12, поэтому мы можем сократить дробь до 1/3, разделив числитель и знаменатель на 12.
Сокращение дроби помогает упростить вычисления и сделать их более удобными для использования. Оно также позволяет нам работать с дробями в их наиболее простой и компактной форме.
Примеры сокращенных дробей
Рассмотрим несколько примеров:
Пример 1:
Даны две дроби: 6/8 и 3/4. Мы видим, что обе дроби имеют общий делитель 2. Сократим обе дроби по этому делителю:
6/8 = 3/4
Теперь мы можем сложить эти дроби без изменения результата:
6/8 + 3/4 = 3/4 + 3/4 = 6/4 = 3/2
Пример 2:
Рассмотрим дроби 12/15 и 4/5. Обе дроби имеют общий делитель 3. После сокращения получим:
12/15 = 4/5
Теперь мы можем сложить эти две дроби:
12/15 + 4/5 = 4/5 + 4/5 = 8/5
Пример 3:
Пусть даны дроби 9/16 и 3/4. Мы видим, что обе дроби также имеют общий делитель 3. После сокращения получаем:
9/16 = 3/4
Теперь мы можем вычесть эти две дроби:
9/16 — 3/4 = 3/4 — 3/4 = 0
Как видим, в этом случае результат равен нулю.
Это всего лишь несколько примеров, которые демонстрируют, что дроби можно сокращать при сложении и вычитании. Это упрощает операции и делает результат более компактным. Однако, в некоторых случаях сокращение дробей может не быть возможным или не привести к упрощению, поэтому всегда следует анализировать каждую конкретную ситуацию.
Видео:Сложение дробей и смешанных чисел. 5 класс.Скачать
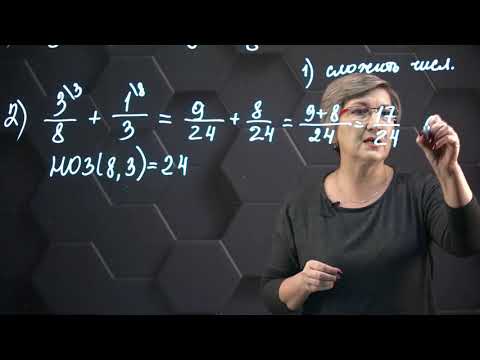
Как сокращать дроби
Для того чтобы сократить дробь, необходимо найти общий делитель числителя и знаменателя и разделить оба эти числа на этот делитель. Общий делитель — это число, которое делит без остатка оба числа.
Сокращение дроби упрощает ее запись и облегчает дальнейшие вычисления. При сложении или вычитании дробей сокращение является важным этапом, так как позволяет получить правильный ответ и избежать возможных ошибок.
Для сокращения дробей можно использовать следующий алгоритм:
- Найти наибольший общий делитель числителя и знаменателя дроби.
- Разделить числитель и знаменатель на этот общий делитель.
- Упростить дробь, если это возможно (например, если числитель и знаменатель делятся на одно и то же число).
Пример:
Дана дробь 12/36. Найдем наибольший общий делитель чисел 12 и 36:
- Делители числа 12: 1, 2, 3, 4, 6, 12.
- Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Наибольший общий делитель для чисел 12 и 36 равен 12. Разделим числитель и знаменатель на этот делитель:
12/36 = 1/3.
Таким образом, дробь 12/36 сократилась до 1/3.
Сокращение дробей является важным и полезным навыком в математике. Подобное упрощение позволяет более эффективно работать с дробными числами и дает возможность получать точные результаты при выполнении математических операций.
Методы сокращения дробей
Существуют несколько методов для сокращения дробей:
- Нахождение общего делителя: Для сокращения дроби необходимо найти наибольший общий делитель (НОД) числителя и знаменателя. Затем дробь делится на НОД, получая новую, сокращенную дробь. Например, для дроби 4/8 НОД равен 4, поэтому после деления числителя и знаменателя на 4, получим сокращенную дробь 1/2.
- Применение простого делителя: Если числитель и знаменатель имеют общий простой делитель, то его можно использовать для сокращения дроби. Например, для дроби 9/27 оба числа имеют простой делитель 3. Поделив числитель и знаменатель на 3, получим сокращенную дробь 1/3.
- Устранение повторяющихся делителей: Иногда числитель и знаменатель могут иметь повторяющиеся делители. В этом случае эти делители могут быть вынесены за скобки и затем сокращены. Например, для дроби 12/36 оба числа имеют повторяющийся делитель 2. Вынося делитель 2 за скобки, получим дробь (2*6)/(2*18). Затем, сократив повторяющийся делитель 2, получим сокращенную дробь 6/18, которая может быть еще сокращена до 1/3.
Важно отметить, что сокращение дробей не меняет их значения. Сокращенная дробь эквивалентна исходной дроби, но может быть более удобной для работы. Поэтому при сложении и вычитании дробей часто рекомендуется сокращать дроби для получения более точных и чистых результатов.
Правила сокращения дробей
| Правило | Пример |
|---|---|
| 1. Если числитель и знаменатель дроби делятся на одно и то же число, то этот делитель можно сократить. | $$\frac{6}{9} = \frac{2 \cdot 3}{3 \cdot 3} = \frac{2}{3}$$ |
| 2. Если числитель и знаменатель дроби не имеют общих делителей, то дробь уже является несократимой. | $$\frac{4}{7}$$ |
| 3. Следует проводить сокращение дроби до несократимого вида. | $$\frac{12}{16} = \frac{2 \cdot 2 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 2} = \frac{3}{4}$$ |
Сокращение дробей является непременным шагом при выполнении арифметических операций с рациональными числами, такими как сложение и вычитание. Правильная сокращенная дробь является более компактной и удобной для дальнейших вычислений.
Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать

Сокращение дробей при сложении и вычитании
Ответ на этот вопрос — «да». Поскольку дроби представляют собой отношение числителя к знаменателю, они остаются равными, если числитель и знаменатель умножить или разделить на одно и то же число.
При сложении и вычитании дробей, часто возникает необходимость привести их к общему знаменателю. Когда это делается, числитель и знаменатель каждой дроби могут быть сокращены по отдельности. Если в результате сокращения числитель и знаменатель не имеют общих делителей, то дробь является сокращенной.
При решении задач с дробями, важно учитывать, что сокращение дробей не изменяет их значения. Сокращенная дробь всегда равна исходной дроби. Однако, процесс сокращения может упростить вычисления и упростить представление результата.
Видео:Как сокращать дроби ( Математика - 5 класс )Скачать

Возможно ли сокращать дроби
Сокращение дроби означает деление ее числителя и знаменателя на их наибольший общий делитель (НОД). Это позволяет представить дробь в наименьшем возможном виде. Однако, при сложении или вычитании, каждая дробь может иметь свой НОД, и сокращение может привести к неверному результату.
В случае, когда знаменатели всех дробей равны между собой, сокращение возможно и не повлияет на результат. Однако, если знаменатели различны, сокращение перед сложением или вычитанием может привести к ошибочным значениям.
Поэтому, чтобы избежать ошибок при сложении и вычитании дробей, рекомендуется сначала выполнить операцию, а затем уже сокращать полученную дробь, если это возможно и необходимо.
Лучший способ узнать, можно ли сокращать дроби при сложении и вычитании, — это проверить знаменатели дробей на наличие общих делителей. Если общих делителей нет, то сокращение не приведет к ошибкам. В противном случае, необходимо сначала выполнить операцию, а затем уже сокращать полученную дробь, если это требуется.
Разные точки зрения
Вопрос о сокращении дробей при сложении и вычитании вызывает различные точки зрения среди математиков и преподавателей.
Одни сторонники утверждают, что дроби следует сокращать до наименьших возможных частей перед выполнением арифметических операций. Они считают, что такой подход позволяет получить наиболее простую и компактную форму ответа, что облегчает дальнейшую работу с ним.
Другие эксперты настаивают на том, что сокращение дробей не является обязательным и может быть выполнено после сложения или вычитания. Они считают, что удлинение и упрощение операций может быть нежелательным и затруднить процесс решения.
Третья группа специалистов признает оба подхода и считает, что выбор между ними зависит от персональных предпочтений и целей решения. Они советуют ученикам и студентам учитывать контекст задачи и целевую аудиторию, чтобы определить, какой подход будет наиболее эффективным.
- Независимо от точек зрения, важно помнить, что при сложении и вычитании дробей следует приводить их к общему знаменателю. Это позволяет проводить арифметические операции с числителями и получать правильные результаты.
- Также стоит отметить, что в некоторых случаях дроби, полученные после сложения или вычитания, могут быть несократимыми. Это происходит, когда числитель и знаменатель не имеют общих делителей, кроме единицы.
- В конечном счете, решение о сокращении или несокращении дробей при сложении и вычитании зависит от личных предпочтений и удобства для выполнения дальнейших операций. Важно понимать принципы и правила математики, чтобы выбрать наиболее эффективный метод для конкретной задачи.
Математические принципы
При сложении и вычитании дробей есть несколько математических принципов, которые помогают нам упростить эти операции и сделать их более удобными для понимания:
1. Для сложения или вычитания дробей их знаменатели должны быть одинаковыми. Если знаменатели различаются, то нужно найти общий знаменатель для всех дробей и привести их к этому общему знаменателю.
2. После приведения дробей к общему знаменателю мы можем складывать или вычитать числители, оставляя знаменатель неизменным.
3. После сложения или вычитания числителей мы можем получить неправильную дробь — дробь, у которой числитель больше знаменателя. В этом случае неправильную дробь можно преобразовать в смешанную дробь, представив ее как сумму целой части и правильной дроби.
4. При сокращении дроби мы можем упростить ее, делая числитель и знаменатель наибольшим образом взаимно простыми числами. Для этого нужно найти наибольший общий делитель числителя и знаменателя и разделить оба числа на него.
Используя эти математические принципы, мы можем упростить сложение и вычитание дробей, делая их более понятными и удобными для работы.
Видео:Сокращение дробей | ПримерыСкачать

Примеры сокращения дробей при сложении и вычитании
Рассмотрим несколько примеров:
Пример 1:
Даны две дроби: 3/6 и 2/4. Их нужно сложить.
Сначала проверим знаменатель. Оба знаменателя равны 6, поэтому нам не нужно ничего изменять.
Теперь сложим числители: 3 + 2 = 5.
Итак, результатом сложения будет дробь 5/6.
Пример 2:
Даны две дроби: 4/9 и 2/3. Их нужно вычесть.
Здесь знаменатели разные, поэтому предварительно нужно привести дроби к общему знаменателю.
Найдем наименьшее общее кратное знаменателей 9 и 3, которым является число 9.
У первой дроби знаменатель уже равен 9, поэтому ничего менять не нужно.
У второй дроби знаменатель нужно умножить на 3, чтобы получить 9: 2/3 * 3/3 = 6/9.
Теперь вычитаем числители: 4 — 6 = -2.
Итак, результатом вычитания будет дробь -2/9.
Таким образом, сокращение дробей при сложении и вычитании позволяет получить более простую форму записи результатов операций и облегчает дальнейшие вычисления.
Конкретные числовые примеры
Для лучшего понимания того, как работает сокращение дробей при сложении и вычитании, рассмотрим несколько конкретных числовых примеров.
Пример 1:
Дано: $\frac{3}{5} + \frac{2}{5}$
Сначала мы суммируем числители: $3 + 2 = 5$
Затем мы оставляем знаменатель неизменным: $5$
Поэтому, $\frac{3}{5} + \frac{2}{5} = \frac{5}{5}$
Затем мы сокращаем полученную дробь, которая равна единице: $\frac{5}{5} = 1$
Ответ: $1$
Пример 2:
Дано: $\frac{4}{9} — \frac{1}{3}$
Сначала мы находим общий знаменатель: $9$ и $3$ делятся на $3$, поэтому общий знаменатель равен $9$
После этого мы приводим дроби к общему знаменателю:
$\frac{4}{9} = \frac{4}{9} \cdot \frac{1}{1} = \frac{4}{9} \cdot \frac{3}{3} = \frac{12}{27}$
$\frac{1}{3} = \frac{1}{3} \cdot \frac{3}{3} = \frac{3}{9}$
Теперь мы можем вычесть дроби: $\frac{12}{27} — \frac{3}{9} = \frac{12 — 3}{27} = \frac{9}{27}$
Затем мы сокращаем полученную дробь: $\frac{9}{27} = \frac{1}{3}$
Ответ: $\frac{1}{3}$
Таким образом, на примерах мы увидели, что сокращение дробей возможно как до операции сложения или вычитания, так и после ее выполнения.
Подробный анализ сокращения
При сложении и вычитании дробей, возникает необходимость нахождения общего знаменателя, чтобы можно было провести операцию. Общий знаменатель – это число, на которое делятся все знаменатели дробей в операции. Например, для сложения дробей 1/3 и 1/4 общим знаменателем будет число 12, так как 3 и 4 на него делятся без остатка.
Теперь рассмотрим вопрос о сокращении дробей при сложении и вычитании. Сокращение дроби происходит, когда числитель и знаменатель имеют общие делители, которые можно сократить. Если общий знаменатель найден, то сложение и вычитание дробей происходит путем сложения (или вычитания) числителей при одинаковом знаменателе. Но если числитель и знаменатель имеют общие делители, то сокращаем дробь, чтобы ответ был в наименьшей форме.
Сокращение дробей осуществляется путем деления числителя и знаменателя на их наибольший общий делитель (НОД). Например, если у нас есть дробь 12/24, то ее можно сократить, разделив числитель и знаменатель на их НОД, который равен 12. После сокращения получим дробь 1/2.
Важно отметить, что сокращение дробей не влияет на результат сложения или вычитания. Результат будет тот же самый, независимо от того, была ли дробь сокращена или нет. Однако сокращение помогает нам получить дробь в наименьшей форме и сделать ее более удобной для работы.
Поэтому, можно осуществлять сокращение дробей при сложении и вычитании, чтобы получить наименьшую форму дроби и упростить ее последующую обработку.
📺 Видео
Вычитание дробей. Как вычитать дроби?Скачать

Сложение дробей и смешанных чисел. Практическая часть. 5 класс.Скачать

Сокращение дробей. 6 классСкачать

МАТЕМАТИКА 6 класс: Сокращение дробей | ВидеоурокСкачать

892 Никольский /Сокращение при умноженииСкачать
АЛГЕБРА с НУЛЯ — Сложение и Вычитание ДробейСкачать

Как умножать и делить дроби (Математика 5 класс)Скачать

Как найти общий знаменатель. Математика 6 класс простоСкачать

сложение и вычитание дробей. 6 класс математикаСкачать

5 класс, 29 урок, Сложение и вычитание смешанных чиселСкачать

Сложение и вычитание дробей с разными знаменателями.Скачать

Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать
