Пирамида в геометрии: определение и свойства (7 видео)

Пирамида — это геометрическое тело, состоящее из плоского многоугольника, называемого основанием, и треугольных граней, соединяющих каждую вершину основания с одной общей вершиной, называемой вершиной пирамиды. Пирамида является одним из основных объектов изучения в геометрии и имеет множество интересных свойств и связей с другими фигурами.

Важным свойством пирамиды является то, что все боковые грани пирамиды являются треугольниками. Кроме того, боковые грани пирамиды имеют одну общую вершину и лежат в одной плоскости. Основание пирамиды может быть различной формы: треугольником, квадратом, пятиугольником и т. д. Величина пирамиды определяется её высотой, радиусом основания и другими параметрами, которые зависят от формы пирамиды.

Пирамида широко используется в математике и физике. В геометрии пирамида используется для изучения объема и площадей поверхностей. Она также является одной из основных фигур при рассмотрении пространственных отношений и преобразований. В физике, пирамиды встречаются в различных контекстах, включая оптику, гравитационную физику и строительство.

Содержание

Определение пирамиды
Структура пирамиды
Типы пирамид
Основные свойства пирамиды
Площадь основания
Объем пирамиды
Дополнительные свойства пирамиды
Высота пирамиды
Углы пирамиды
💥 Видео

Видео:Пирамида. 11 класс.Скачать

Определение пирамиды

Сама идея пирамиды возникла в результате стремления человека возвыситься над окружающим миром и приблизиться к небесам. Поэтому пирамиды часто ассоциируются со святыми и мистическими сооружениями различных древних цивилизаций.

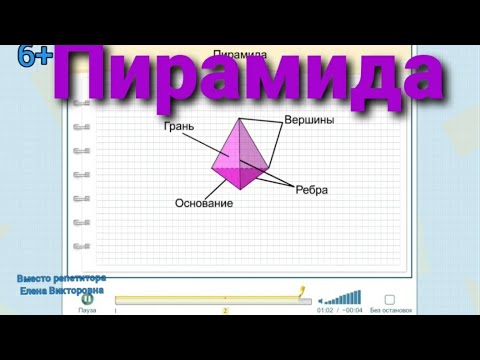
Структура такого многогранника состоит из основания и боковых граней. Основание образует нижнюю часть пирамиды, а боковые грани соединяют вершину с каждой точкой основания. Вершина пирамиды является единственной и возвышается над основанием.

В зависимости от формы основания и положения вершины, пирамиды могут иметь различные типы, такие как треугольные пирамиды, квадратные пирамиды, правильные пирамиды и другие.

Основными свойствами пирамиды являются площадь основания и объем. Площадь основания рассчитывается в зависимости от формы и размеров основания пирамиды, а объем определяется как объем покрывающего пирамиду пространства.

Пирамиды также обладают дополнительными характеристиками, такими как высота, которая представляет собой расстояние от вершины до плоскости основания, и углы пирамиды, которые зависят от формы ее основания.

В целом, пирамиды представляют собой интересные геометрические фигуры, которые не только имеют свои математические свойства, но и являются символами различных культур и исторических периодов.

Структура пирамиды

Основание пирамиды — это многоугольник, который является нижней плоской частью пирамиды. Оно может быть любой формы: треугольник, квадрат, прямоугольник, пятиугольник и так далее.

Высота пирамиды — это отрезок перпендикуляра, опущенный из вершины пирамиды на плоскость основания. Она обозначается символом «h». Высота пирамиды определяет расстояние от вершины до основания и влияет на объем и площадь пирамиды.

Боковые грани пирамиды — это треугольники, образованные ребрами, которые соединяют вершину пирамиды с вершинами основания. Число боковых граней зависит от числа вершин основания.

Вершина пирамиды — это точка, которая является концом всех ребер пирамиды. Эта точка находится выше основания и соединена с каждой вершиной основания ребрами. Вершина пирамиды обозначается символом «V».

Таким образом, структура пирамиды включает основание, высоту, боковые грани и вершину. Все эти элементы взаимосвязаны и определяют форму и свойства пирамиды.

Типы пирамид

В геометрии существует несколько различных типов пирамид, которые отличаются своей формой и структурой.

1. Треугольная пирамида — это пирамида, у которой основание представляет собой треугольник. Все боковые грани такой пирамиды являются треугольниками.

2. Четырехугольная пирамида — такая пирамида имеет основание в виде четырехугольника, а боковые грани представляют собой треугольники или четырехугольники.

3. Правильная пирамида — это пирамида, у которой основание является правильным многоугольником (таким как равносторонний треугольник или квадрат). Все боковые грани правильной пирамиды являются равными треугольниками.

4. Неправильная пирамида — это пирамида, у которой основание представляет собой неправильный многоугольник (такой как произвольный треугольник или четырехугольник). Боковые грани неправильной пирамиды также могут быть неправильными треугольниками или четырехугольниками.

Каждый из этих типов пирамид имеет свои уникальные свойства и характеристики, которые могут быть использованы при решении геометрических задач и расчетах.

Видео:10 класс, 32 урок, ПирамидаСкачать

Основные свойства пирамиды

Основные свойства пирамиды включают в себя площадь основания и объем пирамиды.

Площадь основания пирамиды — это площадь фигуры, на которой пирамида устоена. Обычно основание пирамиды представляет собой многоугольник. Для расчета площади основания нужно знать его форму и размеры сторон. Для прямоугольной пирамиды площадь основания вычисляется по формуле: площадь = длина * ширина.

Объем пирамиды — это количество пространства, занимаемого пирамидой. Объем пирамиды вычисляется по формуле: объем = (площадь основания * высота) / 3. Здесь высота пирамиды — это расстояние от вершины до плоскости основания, а площадь основания вычисляется в соответствии с формулой, описанной выше.

Зная площадь основания и высоту пирамиды, можно рассчитать ее объем, что может быть полезно при решении задач в геометрии и строительстве.

Таким образом, основные свойства пирамиды — это ее площадь основания и объем пирамиды, которые могут быть использованы для расчета и анализа данной геометрической фигуры.

Площадь основания

Для нахождения площади основания необходимо знать ее форму и измерения сторон или радиуса в случае круглого основания. Например, для квадратной пирамиды площадь основания вычисляется, как квадрат длины одной из сторон основания: S = a^2, где a — длина стороны.

Если основание пирамиды не является регулярной фигурой, то площадь основания может быть найдена с помощью соответствующей формулы, учитывающей форму и величину сторон или радиуса основания.

Площадь основания важна для определения объема пирамиды и рассмотрения ее свойств и характеристик. Она также может быть использована в различных практических задачах, например, при расчете площади участка земли или площади основы строений, имеющих пирамидальную форму.

Объем пирамиды

V = (1/3) * S * h,

где V — объем, S — площадь основания, h — высота пирамиды.

Для вычисления объема пирамиды необходимо знать площадь основания и высоту. Площадь основания может быть вычислена с использованием соответствующей формулы, а высота может быть измерена или задана в условии задачи.

Особенно интересно, что объем пирамиды составляет одну треть от объема соответствующей прямоугольной призмы с той же площадью основания и высотой. Это означает, что пирамида занимает меньшее пространство по сравнению с призмой, имея одинаковые размеры основания и высоту.

Знание объема пирамиды может быть полезным в различных областях, включая геометрию, архитектуру и инженерное дело. Например, зная объем пирамиды и площадь основания, можно рассчитать количество материала, необходимого для постройки пирамиды или определить ее вместимость для различных целей.

Таким образом, понимание и вычисление объема пирамиды являются важными навыками, которые могут быть применены в различных сферах деятельности и решении задач разного уровня сложности.

Видео:Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Дополнительные свойства пирамиды

Помимо основных свойств, у пирамиды есть еще несколько дополнительных характеристик, которые могут быть полезными при решении геометрических задач.

Одним из таких свойств является высота пирамиды. Высота – это вертикальное расстояние от вершины пирамиды до основания. Она проходит через центр основания и перпендикулярна ему. Высота пирамиды может быть использована для вычисления ее объема или площади боковой поверхности.

Еще одним интересным свойством пирамиды являются ее углы. У пирамиды могут быть различные типы углов: углы между боковыми гранями, углы между ребрами и другие. Знание этих углов может помочь в определении формы и размеров пирамиды, а также в доказательстве различных геометрических утверждений.

Дополнительные свойства пирамиды могут быть использованы для решения сложных геометрических задач и представляют собой важную информацию о ее структуре и характеристиках. Изучение этих свойств позволяет более глубоко понять и анализировать геометрические объекты, а также применять полученные знания в практических ситуациях.

В итоге, дополнительные свойства пирамиды являются неотъемлемой частью ее описания и играют важную роль в геометрии.

Высота пирамиды

Высота пирамиды можно найти различными способами, в зависимости от известных данных и требуемой точности. Наиболее распространенные методы включают использование теоремы Пифагора, подобия треугольников или тригонометрических функций.

В ряде случаев высота пирамиды может быть непосредственно измерена с помощью специального оборудования или инструментов, таких как лазерный дальномер или уровень.

Знание высоты пирамиды позволяет решать различные задачи, связанные с ее геометрическими свойствами, обьемом, площадью поверхности, а также использовать в дальнейших расчетах и моделировании.

Углы пирамиды

У пирамиды имеется вершина, от которой отходят боковые грани. Углы пирамиды могут быть и вершинными углами – углами между боковыми гранями, и углами в основании пирамиды.

Вершинные углы пирамиды могут быть различными величинами, в зависимости от формы пирамиды и взаимного расположения плоскостей.

Углы в основании пирамиды также могут иметь различные значения. Например, у правильной пирамиды, основанием которой является правильный многоугольник, углы в основании будут равными между собой.

Углы пирамиды играют важную роль при рассмотрении различных свойств этой геометрической фигуры. Они могут быть использованы для вычисления площади боковых граней, определения объема пирамиды и других характеристик.

Важно отметить, что углы пирамиды могут быть как острыми, так и тупыми. От этого зависит форма и геометрические свойства пирамиды.