Логарифм — математическая функция, обратная экспоненте и широко применяемая в различных областях науки и техники. Однако, перед тем как углубляться в основы логарифма, необходимо понять его структуру и основные составляющие.
Основной составляющей логарифма является основание логарифма. Оно определяет, к какой системе отсчета относительно экспоненты принадлежит логарифмическая шкала. Например, если основание логарифма равно единице, то логарифм будет равным нулю, так как 1 в любой степени равно 1. Основание логарифма может быть любым положительным числом, кроме единицы, что открывает огромные возможности применения логарифма в различных областях.
Другой основной составляющей логарифма является аргумент логарифма. Аргументом называется число, относительно которого мы вычисляем логарифм. Это может быть любое положительное число, но при этом аргумент логарифма должен быть строго больше нуля. В противном случае логарифм будет неопределенным.
- Логарифм: основная концепция и его применение
- Определение логарифма
- Математическое определение логарифма
- Особенности логарифмической функции
- Основные свойства логарифма
- Свойство логарифма суммы
- Свойство логарифма произведения
- Свойство логарифма степени
- Основные правила логарифма
- Правило замены основания логарифма
- Правило сокращения логарифмов
- Правило изменения знака логарифма
- Приложения логарифма в математике и науке
- Логарифмические уравнения
- Логарифмическая шкала и ее использование
- Применение логарифма в статистике
- 🔍 Видео
Видео:Основные свойства логарифмов в одном треке!Скачать
Логарифм: основная концепция и его применение
Логарифмы широко применяются в различных областях науки и инженерии, таких как физика, химия, биология, экономика и многие другие. Они используются для упрощения сложных математических выражений, в алгоритмах и моделях, а также для измерения и анализа данных.
Изначально логарифмы были введены как способ упрощения умножения и деления больших чисел. Например, если нужно умножить два числа, их логарифмы складываются, а затем их сумма извлекается из таблицы логарифмов. Такой подход позволял значительно упростить вычисления.
В настоящее время логарифмы используются для решения различных задач. В физике они помогают описывать законы зависимости величин друг от друга. В экономике логарифмическая шкала используется для избегания искажений при анализе данных с разной величиной. В биологии и медицине логарифмическая шкала используется для оценки интенсивности процессов или концентрации веществ. В компьютерных науках логарифмы используются для измерения сложности алгоритмов и эффективности программного кода.
Таким образом, логарифмы являются важным инструментом в математике и различных научных дисциплинах. Их основная концепция заключается в применении обратной функции к экспоненциальной и использовании логарифмической шкалы для упрощения и анализа сложных явлений и данных.
Видео:Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать
Определение логарифма
Логарифм имеет множество применений в различных областях науки и инженерии. Например, в математике логарифмы используются для упрощения сложных функций, решения уравнений и построения графиков. В физике логарифмические шкалы используются для измерения амплитуды звука или электрического сигнала.
Логарифмы имеют ряд важных свойств, которые позволяют упростить вычисления:
| Операция | Свойство |
|---|---|
| Умножение | \(\log_{a}(b \cdot c) = \log_{a} b + \log_{a} c\) |
| Деление | \(\log_{a}\left(\frac{b}{c} ight) = \log_{a} b — \log_{a} c\) |
| Возведение в степень | \(\log_{a}(b^{c}) = c \cdot \log_{a} b\) |
Наиболее распространенными основаниями логарифма являются 10 (\(\log_{10}\)) и \(e\) (натуральный логарифм \(\log_{e}\)). В научных и инженерных расчетах также широко используется двоичный логарифм (\(\log_{2}\)), который особенно полезен при работе с компьютерами и информационными технологиями.
Математическое определение логарифма
Математическое определение логарифма включает в себя следующие основные составляющие:
- Основание логарифма – это число, возводя которое в степень, получаем показатель. Обычно в математике используют логарифмы с основанием 10 (обычный логарифм), основанием e (натуральный логарифм) или любым другим заданным числом.
- Аргумент логарифма – это число, для которого находим логарифм. Оно должно быть положительным, исключение составляют комплексные числа.
- Значение логарифма – это результат вычисления логарифма для заданного аргумента.
Логарифмы широко применяются в различных областях науки и техники, таких как математика, физика, экономика, астрономия и др. Они позволяют сократить сложные вычисления и упростить представление данных.
Особенности логарифмической функции
- У логарифма есть основание, которое определяет, какую систему чисел мы используем. Наиболее распространенными основаниями являются естественное основание (e) и десятичное основание (10).
- Логарифмическая функция всегда имеет базис, который является аргументом логарифма. Базис должен быть положительным числом и не может быть равен 1.
- Логарифмы могут использоваться для решения уравнений, связанных с экспоненциальным ростом или убыванием. Они позволяют найти неизвестное значение, если известны значения функции и базиса.
- Логарифмическая функция обладает свойством сжатия, что означает, что значения функции с логарифмическим основанием более высокие при малых значениях базиса и наоборот.
- Логарифмическая функция имеет асимптоту, которая является вертикальной линией, которую график функции стремится приближаться, но никогда не пересекает.
Понимание особенностей логарифмической функции является важным для решения различных математических и научных проблем. Они также используются в статистике, физике, экономике и других областях исследований.
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать
Основные свойства логарифма
Логарифм имеет несколько основных свойств, которые помогают в его использовании:
- Свойство произведения: логарифм произведения двух чисел равен сумме логарифмов этих чисел. Из свойства logb(xy) = logb(x) + logb(y) следует, что логарифмом произведения чисел является сумма их логарифмов.
- Свойство степени: логарифм числа, возведенного в степень, равен произведению степени и логарифма этого числа. То есть logb(xn) = n * logb(x).
- Свойство извлечения корня: логарифм корня числа равен частному логарифма числа и показателя корня. То есть logb(√x) = logb(x) / 2.
Используя эти основные свойства логарифма, можно упростить сложные выражения и решить уравнения, связанные с показательными функциями.
Свойство логарифма суммы
Логарифм имеет свойство, что логарифм от произведения двух чисел равен сумме их логарифмов:
Если a и b — положительные числа и c — положительное число, то выполняется следующее равенство:
logc(a * b) = logc(a) + logc(b)
Это свойство может быть использовано для упрощения расчетов и преобразования сложных выражений с помощью логарифмов.
Свойство логарифма произведения
Свойство логарифма произведения гласит, что логарифм произведения двух чисел равен сумме логарифмов этих чисел:
| Логарифм | ||
| Аргумент | Модификация | Пояснение |
| log(x * y) | log(x) + log(y) | Сумма логарифмов отдельных множителей |
Например, если у нас есть выражение log(2 * 5), то мы можем применить свойство логарифма произведения и записать его как log(2) + log(5). Это свойство может быть очень полезно при работе с большими числами или сложных выражениях.
Следует помнить, что это свойство применимо только к логарифмам с одинаковым основанием.
Таким образом, свойство логарифма произведения облегчает вычисления и упрощает решение уравнений, позволяя разбить выражения на более простые составляющие.
Свойство логарифма степени
Свойство логарифма степени гласит, что логарифм степени числа равен произведению степени логарифма этого числа. То есть, если у нас есть число $a$, его логарифм по основанию $b$, и мы находимся в степени $c$, то логарифм степени равен $c$ умноженному на логарифм числа $a$ по основанию $b$.
Например, если у нас есть число $2$, его логарифм по основанию $10$ равен $0.3010$, и мы находимся в степени $3$, то логарифм степени будет равен $3 \times 0.3010 = 0.9030$.
Свойство логарифма степени можно использовать для упрощения вычислений и записи чисел в более удобной форме.
Видео:Логарифмическая функция, ее свойства и график. 11 класс.Скачать
Основные правила логарифма
Вот некоторые из основных правил логарифма:
| Правило | Формула | Пример |
|---|---|---|
| Формула изменения основания логарифма | \( \log_a{b} = \frac{{\log_c{b}}}{{\log_c{a}}} \) | \( \log_2{8} = \frac{{\log_{10}{8}}}{{\log_{10}{2}}} \) |
| Формула произведения | \( \log_a{b \cdot c} = \log_a{b} + \log_a{c} \) | \( \log_3{12} = \log_3{4} + \log_3{3} \) |
| Формула деления | \( \log_a{\frac{b}{c}} = \log_a{b} — \log_a{c} \) | \( \log_2{\frac{8}{4}} = \log_2{8} — \log_2{4} \) |
| Формула возведения в степень | \( \log_a{b^n} = n \cdot \log_a{b} \) | \( \log_2{8^2} = 2 \cdot \log_2{8} \) |
| Формула корня | \( \log_a{\sqrt[n]{b}} = \frac{1}{n} \cdot \log_a{b} \) | \( \log_2{\sqrt[3]{8}} = \frac{1}{3} \cdot \log_2{8} \) |
| Формула изменения основания логарифма на десятичный | \( \log_a{b} = \frac{{\log_{10}{b}}}{{\log_{10}{a}}} \) | \( \log_3{27} = \frac{{\log_{10}{27}}}{{\log_{10}{3}}} \) |
Это лишь несколько примеров основных правил логарифма, которые помогают упростить вычисления и решение задач. Знание и умение применять эти правила является важным инструментом при работе с логарифмами.
Правило замены основания логарифма
Логарифмы можно взять по различным основаниям, обычно мы используем основание 10 или основание $e$. Однако иногда может возникнуть необходимость переходить от одного основания логарифма к другому.
Для этого применяется правило замены основания логарифма. Если имеется логарифм $y$ по основанию $a$, то его можно записать как логарифм $x$ по основанию $b$:
$\log_a y = \frac{{\log_b y}}{{\log_b a}}$
Таким образом, если у нас есть логарифм по известному основанию, мы можем перейти к логарифму по другому основанию, используя это правило.
Например, рассмотрим логарифм по основанию 10. Если нам нужно взять логарифм числа по основанию 2, мы можем воспользоваться правилом замены основания и записать его как:
$\log_2 y = \frac{{\log_{10} y}}{{\log_{10} 2}}$
Таким образом, мы можем перевести логарифм по основанию 2 в логарифм по основанию 10.
Правило замены основания логарифма очень полезно в различных математических и научных расчетах, позволяя переходить от одного основания логарифма к другому.
Правило сокращения логарифмов
Для сокращения логарифмов необходимо знать несколько ключевых свойств логарифмических функций. Во-первых, логарифмическая функция обладает свойством логарифма произведения, которое гласит:
| logb(a * c) = logb(a) + logb(c) |
Это свойство позволяет разбить выражение, содержащее произведение, на сумму двух логарифмов. Таким образом, мы можем сократить сложное выражение до более простой формы.
Во-вторых, логарифмическая функция также обладает свойством логарифма частного, которое гласит:
| logb(a / c) = logb(a) — logb(c) |
Это свойство позволяет разбить выражение, содержащее частное, на разность двух логарифмов. Таким образом, мы можем сократить сложное выражение до более простой формы.
Применение этих двух свойств позволяет сократить любое сложное выражение с логарифмами до более простой и компактной формы. Сокращение логарифмов может быть использовано для более удобных и эффективных вычислений в различных областях, таких как математика, физика, инженерия и т.д.
Правило изменения знака логарифма
Оно утверждает, что если аргумент логарифма принадлежит интервалу от 0 до 1, то значение логарифма будет отрицательным. То есть, если $0 < x < 1$, то $\log_a x < 0$.
Например, если взять некоторое число $x$, такое что $0 < x < 1$, и вычислить логарифм этого числа по основанию $a$, то результат будет отрицательным числом.
Например:
$\log_2 \frac{1}{2} = -1$
$\log_{10} \frac{1}{100} = -2$
Это правило можно использовать, чтобы определить знак логарифма, если известно значение аргумента.
Изменение знака логарифма имеет важное значение при решении уравнений и неравенств, содержащих логарифмы. Оно позволяет учитывать различные случаи и получить все возможные значения логарифма.
Помните, что значением логарифма является показатель степени, к которому нужно возвести основание, чтобы получить аргумент логарифма. Изменение знака логарифма отражает соотношение между основанием и аргументом.
Видео:Логаримы для чайников с нуля — Как решать Логарифмы?Скачать
Приложения логарифма в математике и науке
1. Компактное представление больших чисел: Логарифмы позволяют нам представлять большие числа в виде более удобного и компактного вида. Например, вместо числа 1 000 000 мы можем написать логарифмическую форму записи — log(10^6) = 6.
2. Решение уравнений с переменными в показателях: Некоторые уравнения могут быть решены с использованием логарифма. Если у нас есть уравнение вида a^x = b, мы можем применить логарифмы с обоих сторон уравнения и решить его относительно x.
3. Моделирование роста и декремента: Логарифмы используются в моделях, описывающих рост или убывание величин. Например, логарифмическая шкала используется в графиках, чтобы показать изменение данных в широком диапазоне значений.
4. Работа с процентами и арифметическими прогрессиями: Логарифмы используются для работы с процентами и арифметическими прогрессиями. Например, если мы знаем, что 2^x = 8, мы можем использовать логарифмы, чтобы найти значение x, которое будет равно 3.
5. Решение дифференциальных уравнений: Логарифмы используются при решении дифференциальных уравнений, которые описывают изменение функций в зависимости от их производных. Путем применения логарифмических функций к уравнению мы можем упростить его решение.
Таким образом, логарифмы имеют широкий спектр применений в математике и науке. Они помогают нам представлять числа в более удобном виде, решать уравнения с переменными в показателях, моделировать различные процессы и решать дифференциальные уравнения.
Логарифмические уравнения
Рассмотрим основные типы логарифмических уравнений:
- Простое логарифмическое уравнение имеет вид loga(x) = b, где a — основание логарифма, x — переменная, b — известное значение. Решением такого уравнения является значение переменной x, для которого loga(x) равно b.
- Логарифмическое уравнение с различными основаниями имеет вид loga(x) = logc(d), где a и c — основания логарифмов, x и d — числа. Решение этого уравнения состоит в нахождении значения переменной x, при котором loga(x) равно logc(d).
- Логарифмическое уравнение с переменным основанием имеет вид logx(a) = b, где x — переменная, a и b — известные числа. Решением такого уравнения является значение переменной x, для которого logx(a) равно b.
- Уравнение суммы (разности) логарифмов имеет вид loga(x) + loga(y) = b. Решение данного уравнения заключается в поиске значений переменных x и y, при которых сумма (разность) их логарифмов равна b.
- Уравнение произведения (частного) логарифмов имеет вид loga(x) * loga(y) = b. Решение такого уравнения заключается в нахождении значений переменных x и y, при которых произведение (частное) их логарифмов равно b.
При решении логарифмических уравнений можно использовать свойства логарифмов, такие как свойства умножения, деления, возведения в степень и преобразования логарифма в экспоненту. Также следует учитывать ограничения на переменные, например, что аргумент логарифма должен быть положительным.
Логарифмическая шкала и ее использование
Логарифмическая шкала представляет собой графическую представление чисел в логарифмической форме. Она широко используется в научных и технических областях для представления данных, которые имеют диапазон значений с большой разницей между ними.
Одним из основных преимуществ логарифмической шкалы является возможность более наглядного отображения данных, у которых различия в масштабах значений слишком велики. Например, при представлении графика с экспоненциальным ростом данных на линейной шкале, кривая может выходить за пределы графика, что делает его нечитаемым. На логарифмической шкале такая кривая может быть представлена в виде прямой линии, что делает ее более понятной и удобной для анализа.
Логарифмическая шкала также находит применение при изображении графиков с большим диапазоном значений. Например, при изображении графика потенциальной энергии молекулы или атома, где разница в значениях энергии может быть между 10^-19 Дж и 10^19 Дж. На логарифмической шкале график может быть удобно изображен, позволяя наблюдать как небольшие, так и очень большие значения на одном графике.
Однако, использование логарифмической шкалы требует определенных навыков и понимания, так как она изменяет отношения и пропорции между значениями. Поэтому, при использовании логарифмической шкалы необходимо быть аккуратным и тщательно анализировать данные, чтобы правильно интерпретировать результаты.
Применение логарифма в статистике
Основной применение логарифма в статистике заключается в преобразовании данных, которые имеют асимметричное распределение, в более симметричное распределение. Это помогает улучшить точность статистических моделей и сделать интерпретацию данных более наглядной.
Одним из распространенных применений логарифма в статистике является логарифмическое преобразование. Это преобразование позволяет снизить влияние больших значений на анализ данных и увеличить различимость малых значений.
Другим применением логарифма в статистике является использование его в регрессионном анализе. Преобразование зависимой и независимой переменной с помощью логарифма позволяет получить более линейную связь между этими переменными и улучшить качество модели.
Также логарифм может быть использован для анализа временных рядов. Применение логарифма позволяет устранить нестационарность и обнаружить скрытые закономерности в данных.
🔍 Видео
Логарифм числа. 11 класс.Скачать
Свойства логарифма. 1 часть. 11 класс.Скачать
Что такое Логарифмы? для ЧайниковСкачать
Логарифмы с нуля за 30 минут. Логарифмы 10 класс ЕГЭ профиль математика | УмскулСкачать
Понятие логарифма Основное логарифмическое тождество Скачать
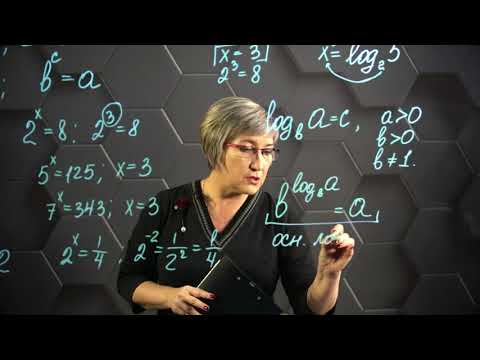
Шпаргалка для школьника — Все Свойства Логарифмов за 15 минутСкачать
Логарифмы в ЕГЭ🫢 Решишь второй?!Скачать
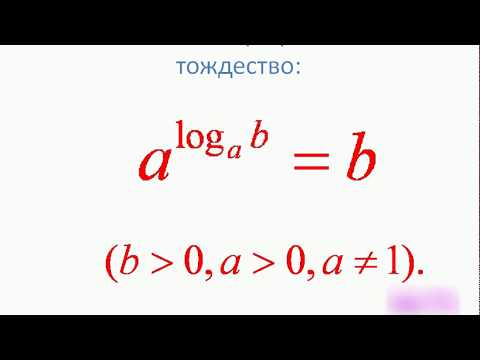
Логарифм. Все свойства логарифмов | Осторожно, спойлер! | Борис Трушин |Скачать
Логарифм числа. Основное логарифмическое тождествоСкачать
СРАВНЕНИЕ ПРОСТЫХ ЧИСЕЛ И ЛОГАРИФМОВ В ЕГЭ #shorts #егэ #огэ #математика #логарифмы #профильныйегэСкачать
Математика это не ИсламСкачать
ВСЯ СЛОЖНОСТЬ АЛГОРИТМОВ ЗА 11 МИНУТ | ОСНОВЫ ПРОГРАММИРОВАНИЯСкачать
Логарифмы в ЕГЭ💥 Второй пример с тебя!Скачать
КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать
11 класс, 14 урок, Понятие логарифмаСкачать
