В геометрии вершина – это точка, в которой пересекаются две или более линии, отрезка, прямоугольника или многоугольника. Вершины играют важную роль в анализе и изучении фигур, так как они определяют основные характеристики и свойства объектов.
Одной из основных особенностей вершин является их количество. Например, у прямоугольника есть четыре вершины, а у квадрата – только одна. Количество вершин влияет на форму фигуры и определяет ее структуру и свойства.
Кроме того, вершины имеют свои координаты на координатной плоскости. Они могут быть заданы числами или буквенными обозначениями. Знание координат вершин позволяет определить положение и расстояние между объектами, а также строить и анализировать геометрические модели.
Вершины также могут быть классифицированы по различным параметрам, таким как углы, которые они образуют, или их взаимное расположение. Это позволяет более детально изучать форму и структуру фигур, а также проводить сравнительный анализ различных объектов.
- Что такое вершина в геометрии?
- Определение вершины
- Значение вершины в геометрии
- Особенности вершины в геометрии
- Многоугольники с вершиной
- Свойства вершины в трехмерной геометрии
- Примеры использования вершины в геометрии
- Построение геометрических фигур
- Определение координат вершины
- Значение вершины в пространстве
- Вершина в геометрии и топологии
- Связь вершины с другими элементами пространства
- 📽️ Видео
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Что такое вершина в геометрии?
Вершины могут быть трехмерными, то есть иметь координаты x, y и z, или двумерными, с координатами x и y. Двумерные вершины выбираются на плоскости, в то время как трехмерные вершины используются для построения тел.
Каждая вершина может быть именована или обозначена буквой. Вершины могут быть соединены ребрами, которые вместе образуют грани фигуры. Количество вершин в фигуре зависит от ее типа и сложности. Некоторые примеры геометрических фигур с вершинами включают треугольник (3 вершины), квадрат (4 вершины), пирамиду (5 вершин) и куб (8 вершин).
Вершины в геометрии играют важную роль в определении формы и свойств фигур. Они помогают анализировать и классифицировать геометрические объекты, а также вычислять их свойства, такие как площадь, объем и периметр. Знание о вершинах помогает решать различные геометрические задачи и применять их в реальной жизни, например, при строительстве, дизайне и моделировании.
Определение вершины
Вершины играют важную роль в геометрии и имеют несколько особенностей:
| Особенность | Описание |
|---|---|
| Количество вершин | Фигуры могут иметь разное количество вершин. Например, треугольник имеет 3 вершины, квадрат — 4 вершины. |
| Расположение вершин | Расположение вершин влияет на форму и тип фигуры. Фигуры с разным расположением вершин могут иметь разные свойства и характеристики. |
| Многогранники | Многогранники состоят из плоских граней и вершин. Каждая вершина многогранника соединяется с несколькими гранями. |
Таким образом, вершины имеют важное значение в геометрии и играют роль в определении формы и особенностей фигур.
Значение вершины в геометрии
Вершины играют важную роль в определении многогранников. Например, в треугольнике вершины соединяются отрезками, называемыми сторонами треугольника. Вершины треугольника также определяют его углы.
Вершины также используются в определении множества прямоугольников, квадратов и параллелограммов. У этих фигур вершины являются концами сторон и местами пересечения.
Вершины полезны не только для определения форм фигур, но и для вычисления их свойств. Например, в остроугольном треугольнике вершины играют ключевую роль в определении высоты и медианы, а также вычислении площади.
В общем, вершины в геометрии являются важными элементами, которые помогают определить формы и свойства различных фигур. Изучение вершин и их связей с другими элементами геометрии позволяет лучше понять многие геометрические концепции и применять их на практике.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Особенности вершины в геометрии
Вершина в геометрии играет важную роль и имеет несколько особенностей.
- Вершина является точкой пересечения двух или более линий или ребер.
- У вершины могут быть разные свойства, такие как углы, длины сторон и радиусы.
- Вершины могут быть острыми, тупыми или прямыми, в зависимости от геометрической формы.
- Вершина может быть плоской или трехмерной, в зависимости от размерности фигуры.
Вершины играют важную роль в определении формы геометрической фигуры и являются ключевыми элементами при решении задач на симметрию, углы и стороны.
Вершины могут использоваться для построения многоугольников, пирамид, параллелограммов и других геометрических фигур.
Важно отметить, что вершина не обладает физическими свойствами, такими как масса или объем, она является одной из абстрактных составных частей геометрических фигур.
Многоугольники с вершиной
Многоугольники с вершиной обладают свойствами, которые делают их интересными и полезными в различных областях математики и реального мира. Одно из основных свойств многоугольников с вершиной состоит в их способности образовывать равносторонние и равнобедренные фигуры.
Например, равносторонний треугольник – это многоугольник с тремя равными сторонами и тремя равными углами. Каждая вершина треугольника является точкой, где пересекаются две стороны, и в треугольнике обычно три вершины.
Равнобедренный треугольник – это многоугольник с двумя равными сторонами и двумя равными углами. Вершины равнобедренного треугольника также являются точками пересечения сторон, и в треугольнике обычно три вершины.
Многоугольники с вершиной широко использованы в геометрии и графике, а также в алгоритмах и программировании. Они могут быть использованы для моделирования геометрических фигур и решения различных задач, связанных с расчетами и конструкциями.
Таким образом, многоугольники с вершиной являются важным понятием в геометрии и математике в целом, и их свойства и особенности представляют интерес и значимость при изучении и применении в различных областях науки и практики.
Свойства вершины в трехмерной геометрии
В трехмерной геометрии вершиной называется точка, в которой пересекаются три или более ребра. Вершины играют важную роль в определении формы и структуры трехмерных объектов, таких как многогранники или сетки.
Свойства вершин в трехмерной геометрии могут быть разнообразными:
- Координаты: каждая вершина имеет свои координаты в трехмерном пространстве, определяющие ее положение относительно осей x, y и z. Координаты вершины могут быть заданы числами или символами.
- Соседние вершины: каждая вершина может иметь связи с другими вершинами, образуя соседствующие пары или группы. Эти связи могут быть использованы для определения поверхностей, ребер или граней.
- Степень: степень вершины — количество ребер, связанных с данной вершиной. Например, вершина с тремя ребрами имеет степень 3. Степень вершины может быть использована для определения различных характеристик исследуемого объекта.
- Эйлерова характеристика: сумма степеней всех вершин в трехмерной геометрии равна числу ребер в данной геометрии.
Изучение свойств вершин позволяет более глубоко понять трехмерные объекты и их структуру. Это важно для различных областей, таких как компьютерная графика, инженерия, архитектура и другие.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Примеры использования вершины в геометрии
- Вершина треугольника: в треугольнике вершины являются его углами. Одна из вершин обычно называется «вершиной A», другая — «вершиной B», а третья — «вершиной C». Вершины определяют положение углов треугольника и могут использоваться для решения геометрических задач.
- Вершина квадрата: в квадрате есть четыре вершины, каждая из которых является углом фигуры. Вершины квадрата регулярно используются для определения его формы и размеров, а также для вычисления периметра и площади.
- Вершина прямоугольника: прямоугольник имеет четыре вершины, каждая из которых является углом фигуры. Вершины прямоугольника играют важную роль при определении его формы и размеров, их использование необходимо при вычислении периметра и площади прямоугольника.
- Вершина многоугольника: многоугольник может иметь любое количество вершин, и каждая из них является углом фигуры. Вершины многоугольника определяют его форму, а их координаты используются для задания положения и размеров фигуры.
- Вершина пирамиды: пирамида имеет вершину, которая является высшей точкой фигуры. Вершина пирамиды играет важную роль при определении ее формы и структуры.
Вершины в геометрии имеют большое значение и широко применяются для определения формы, размеров и структуры различных фигур.
Построение геометрических фигур
Геометрические фигуры можно строить с использованием различных методов и инструментов. В основе построения фигур лежат простые геометрические принципы и правила, которых нужно придерживаться.
Для построения геометрических фигур обычно используют геометрические инструменты, такие как линейка, циркуль, угольник. Они позволяют точно измерять отрезки, строить окружности, углы и другие элементы геометрии.
Одним из способов построения геометрических фигур является метод компаса и линейки. Для этого необходимо выбрать две точки и провести отрезок между ними с помощью линейки, а затем с помощью компаса построить окружность с центром в одной из точек и радиусом, равным длине отрезка.
Кроме того, с помощью угольника можно проводить прямые линии под определенным углом. Для этого нужно установить угольник между двумя точками и провести линию вдоль одного из его граней.
Для построения многоугольников можно использовать метод последовательного соединения отрезков. Необходимо выбрать точки, соединив их отрезками, и таким образом построить фигуру с нужным количеством сторон.
При построении геометрических фигур необходимо быть аккуратным и точным, чтобы избежать ошибок. Нужно следить за соответствием сторон и углов заданным значениям, а также измерять отрезки и углы с помощью геометрических инструментов.
Определение координат вершины
Определение координат вершины зависит от типа фигуры и системы координат, используемой в конкретной задаче. В системе координат, основанной на плоскости, вершины обычно задаются парой чисел (x, y), где x — координата по горизонтальной оси (ось абсцисс) и y — координата по вертикальной оси (ось ординат).
Для примера, рассмотрим треугольник ABC:
- Вершина A имеет координаты (xA, yA).
- Вершина B имеет координаты (xB, yB).
- Вершина C имеет координаты (xC, yC).
В случае, если треугольник ABC является прямоугольным, вершина C может быть найдена с использованием теоремы Пифагора или других соответствующих геометрических свойств.
Для других фигур, например, квадрата или прямоугольника, координаты вершин могут быть менее сложными и задаются просто в виде угла и длины стороны.
Важно помнить, что определение координат вершины зависит от выбранной системы координат и может отличаться в разных задачах и представлениях геометрических фигур.
Видео:Теория вероятностей | Математика TutorOnlineСкачать

Значение вершины в пространстве
Вершины в пространстве играют ключевую роль в определении формы и структуры трехмерных объектов. Они помогают определить линии, грани и объемы. Вершины в трехмерном пространстве могут быть использованы для описания и моделирования таких объектов, как полигоны, многогранники, а также движущиеся тела в пространстве.
Вершины в пространстве могут иметь различные особенности. Например, они могут быть выпуклыми, когда все углы между ребрами меньше 180 градусов, или вогнутыми, когда хотя бы один угол больше 180 градусов. Вершины также могут быть точками пересечения линий или поверхностей.
Значение вершины в пространстве заключается в ее возможности создавать трехмерные объекты. Она является ключевым элементом при построении и анализе трехмерных моделей. Правильное определение и понимание вершин помогает визуализировать объекты в трехмерном пространстве и раскрыть их структуру и форму.
Вершины в пространстве также имеют значение в практических областях, таких как графика компьютерных игр, архитектура, инженерное моделирование и дизайн. Они позволяют создавать сложные трехмерные модели, представлять их визуально и выполнять различные операции над ними.
Вершина в геометрии и топологии
В геометрии вершина обычно определяется как точка, в которой пересекаются стороны многоугольника или ребра многогранника. Она является краеугольным камнем построения геометрических фигур. Вершины могут быть трехмерными в пространстве или двумерными на плоскости.
В топологии вершина определяется как точка, которая окружена окрестностью. Вершины в топологии образуют топологические пространства и могут быть использованы для определения свойств топологических фигур. Например, вершины могут быть использованы для определения числа связных компонентов.
Вершины играют важную роль в геометрии и топологии, так как они помогают определить форму и структуру объектов. Их положение и количество могут влиять на свойства и характеристики фигур. Понимание понятия вершины позволяет более глубоко изучать и анализировать геометрические и топологические объекты.
Связь вершины с другими элементами пространства
Первая связь вершины – это связь с линиями и отрезками. Если в вершине пересекаются две линии или отрезка, они называются смежными линиями или отрезками. При этом вершина является их общей точкой и определяет их положение относительно друг друга.
Вторая связь вершины – это связь с гранями. Грань – это плоская фигура, ограниченная линиями. Если грань имеет общую вершину с другой гранью, они называются смежными гранями. Их общая вершина определяет пространственное расположение данных граней и их взаимосвязь.
Третья связь вершины – это связь с объемами и телами. Объем – это трехмерная фигура, которая имеет высоту, ширину и длину. Если вершина является общей для двух или более объемов или тел, их называют смежными объемами или телами. Вершина определяет пространственное положение и взаимосвязь этих объемов.
Связь вершины с другими элементами пространства играет важную роль в геометрии. Она помогает определить положение объектов и их взаимосвязь, что позволяет строить и анализировать геометрические структуры и фигуры.
📽️ Видео
ВЕРШИНА - что это такое? значение и описаниеСкачать

Уравнения стороны треугольника и медианыСкачать

Графы, вершины, ребра, инцидентность, смежностьСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

ВЕРШИНЫ И СТОРОНЫ МНОГОУГОЛЬНИКАСкачать

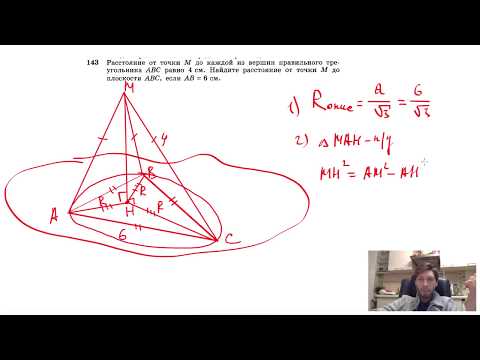
№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать
Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

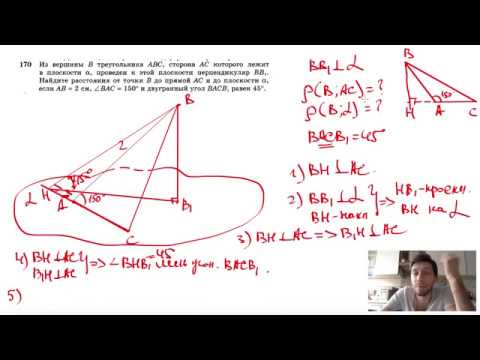
№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать
КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Подсчёт количества граней и рёбер у трёхмерных фигур | Фигура | ГеометрияСкачать

№239. Докажите, что в треугольнике медиана не меньше высоты, проведенной из той же вершины.Скачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Вычисляем высоту через координаты вершин 1Скачать
