Куб — это одна из наиболее простых и известных геометрических фигур. Он представляет собой геометрическое тело, у которого все ребра равны по длине. Однако, при изучении куба возникает вопрос о его длине. Как определить длину куба и какая формула используется для её вычисления? В данной статье мы рассмотрим эти вопросы и изучим основные свойства длины куба.
Длина куба определяется по длине его ребра. Ребро куба — это отрезок, соединяющий две соседние вершины куба. Все ребра куба имеют одинаковую длину, поэтому длину куба можно определить, зная длину одного из его рёбер. Формула для вычисления длины куба проста и понятна: длина куба равна произведению длины одного из его рёбер на 12.
Основное свойство длины куба заключается в том, что все его рёбра равны и параллельны друг другу. Это свойство делает куб одним из наиболее симметричных тел. Куб имеет также свойство самопересечения: пересекая себя, он образует 12 ребер, 8 вершин и 6 граней. Это отличительные особенности куба, важные для его изучения и применения в различных областях знаний.
Видео:5 класс, 21 урок, Объемы. Объем прямоугольного параллелепипедаСкачать

Что такое длина куба?
Для куба все стороны равны между собой, поэтому его длина является мерой размерности этой фигуры. Она может быть измерена в сантиметрах, метрах или других единицах измерения длины.
Формула для вычисления длины куба проста: длина равна длине одной из его сторон, так как все стороны куба равны. Например, если одна сторона куба равна 5 сантиметрам, то длина куба составит 5 сантиметров.
Запомните следующую формулу: длина куба = длина стороны куба.
Зная длину куба, можно определить и другие характеристики этой фигуры, такие как объем и площадь его поверхности. Для расчета объема куба необходимо возвести длину его стороны в третью степень.
Таким образом, понимание длины куба является важным базовым понятием в геометрии и математике в целом. Она позволяет определить размеры этой фигуры и проводить различные расчеты связанные с кубом.
Видео:КАК НАЙТИ ДЛИНУ ВСЕХ РЕБЕР КУБА? Примеры | МАТЕМАТИКА 5 классСкачать

Определение и свойства
Куб — это особый вид геометрического объекта, который имеет все стороны одинаковой длины. Таким образом, длина куба определяет длину каждой его стороны.
Свойства длины куба:
1. Все стороны куба имеют одинаковую длину. Это означает, что если мы знаем длину одной стороны куба, мы автоматически знаем длину остальных его сторон.
2. Длина куба может быть измерена. С помощью линейки или другого инструмента измерения можно определить длину куба.
3. Длина куба может быть изменена. Путем изменения размера куба можно изменить его длину. Например, если увеличить размер одной из сторон куба, длина куба также увеличится.
4. Длина куба важна для вычислений. Например, для вычисления объема куба необходимо знать его длину, так как объем куба равен длине каждой стороны, возведенной в квадрат.
Таким образом, длина куба является основным параметром, который определяет его форму и позволяет проводить различные расчеты и измерения.
Определение длины куба
Для рассчета длины куба необходимо учитывать масштаб и единицы измерения, которые используются. В общем случае, длина куба может быть выражена через сторону куба по формуле:
Длина = Сторона × √3
Где сторона — длина стороны куба.
Свойства куба, связанные с его длиной, включают:
- Все ребра куба имеют одинаковую длину.
- Длина диагонали куба равна √3 умножить на длину его ребра.
- Длина куба может быть измерена с использованием линейки, меры или другого подходящего инструмента.
Важно отметить, что длина куба является линейной мерой и может быть выражена в различных единицах измерения, таких как сантиметры, метры, футы и т.д. В зависимости от контекста, указывается соответствующая единица измерения.
Свойства длины куба
1. Все ребра куба имеют одинаковую длину. Это свойство позволяет нам определить длину куба одним числом, а не вычислять длину каждого его ребра отдельно.
2. Длина куба является мерой его размера в одном направлении. Это означает, что длина куба определяется только его габаритными размерами вдоль одной из осей — длиной, шириной или высотой.
3. Длина куба соотносится с другими его геометрическими характеристиками. Например, площадь куба вычисляется по формуле L^2, где L — длина ребра куба. Объём куба вычисляется по формуле L^3, где L — длина ребра куба.
4. Длина куба может использоваться для определения других параметров, таких как площадь его боковой поверхности или длина его диагонали.
Изучение свойств длины куба позволяет более глубоко понять его геометрическую структуру и использовать эту информацию в различных математических и инженерных расчетах.
| Свойство | Описание |
|---|---|
| 1 | Все ребра куба имеют одинаковую длину. |
| 2 | Длина куба является мерой его размера в одном направлении. |
| 3 | Длина куба соотносится с другими его геометрическими характеристиками. |
| 4 | Длина куба может использоваться для определения других параметров. |
Видео:Математика 5 Объем Объем прямоугольного параллелепипедаСкачать

Как вычислить длину куба?
- Умножьте длину одной из граней на корень квадратный из 3.
Таким образом, формула для вычисления длины куба представляет собой:
Где — длина одной из граней куба.
Свойства длины куба:
- Длина куба является физической величиной, измеряемой в линейных единицах (например, метрах).
- Длина куба всегда будет положительной величиной, так как не может быть отрицательных граней или расстояний.
- Длина куба может быть применена не только к физическим объектам, но и к абстрактным величинам, таким как числа или математические объекты.
Вычисление длины куба является важной задачей в геометрии, физике и множестве других областей. Знание длины куба позволяет определить его объем, площадь поверхности и многое другое.
Видео:КАК НАЙТИ ОБЪЕМ КУБА ПО РЕБРУ? Примеры | МАТЕМАТИКА 5 классСкачать

Формула
Для вычисления длины ребра куба используется основная формула:
Длина куба = a
где a — длина ребра куба.
Эта формула говорит нам о том, что длина куба равна длине его ребра.
Формула для вычисления длины куба
Для определения длины куба используется простая формула:
Длина куба (L) равна ребру куба (a), умноженному на 4:
L = 4a
Таким образом, чтобы вычислить длину куба, необходимо знать длину одной из его сторон (ребро) и умножить её на 4.
Знание формулы для вычисления длины куба позволяет упростить процесс измерения и оценки размеров куба. Она может быть полезной в различных задачах, связанных с геометрией и строительством.
Пример расчета длины куба
Расчет длины куба может быть произведен с использованием формулы, учитывающей его особые свойства. Для этого необходимо знать длину ребра куба.
- Предположим, у нас есть куб с ребром длиной 5 сантиметров.
- В формуле для расчета длины куба используется умножение длины ребра на 12.
- Таким образом, мы можем рассчитать длину куба следующим образом: 5 сантиметров * 12 = 60 сантиметров.
Таким образом, длина куба с ребром длиной 5 сантиметров равна 60 сантиметров.
Видео:Длина окружности. Математика 6 класс.Скачать

Значение длины куба в геометрии
Длина куба определяется как расстояние между противоположными вершинами, проходящее по одной из его сторон. Для куба с длиной стороны a, его длина равна a.
Длина куба является одним из важных свойств этой фигуры. Благодаря равным сторонам, куб обладает рядом особых свойств:
- Симметрия: Куб имеет множество осей симметрии, проходящих через его центр и соединяющих противоположные вершины. Благодаря этому свойству, куб выглядит одинаково со всех сторон.
- Объем: Длина куба влияет на его объем, который определяется формулой V = a^3, где a — длина стороны куба.
- Площадь поверхности: Длина куба также влияет на его площадь поверхности, которая определяется формулой S = 6a^2, где a — длина стороны куба.
- Диагональ: Длина куба связана с длиной его диагонали, которая определяется формулой d = a * √3, где a — длина стороны куба.
Значение длины куба в геометрии играет важную роль при рассмотрении различных свойств и параметров этой геометрической фигуры. Оно определяет внешний вид и размеры куба, а также его объем и площадь поверхности.
🌟 Видео
Длина окружности. Площадь круга. 6 класс.Скачать

Формула объёма прямоугольного параллелепипеда (для 3В)Скачать

КАК НАЙТИ ПЛОЩАДЬ ПОВЕРХНОСТИ КУБА, ЕСЛИ ИЗВЕСТНО РЕБРО? Примеры | МАТЕМАТИКА 5 классСкачать

Математика 4 класс (Урок№62 - Куб.)Скачать

КАК НАЙТИ ПЛОЩАДЬ ПОВЕРХНОСТИ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА? Примеры | МАТЕМАТИКА 5 классСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Куб. Кубики. Форма, грани, ребра, объем кубаСкачать

Площадь прямоугольника. Как найти площадь прямоугольника?Скачать

КАК НАЙТИ РЕБРО КУБА, ЗНАЯ ЕГО ОБЪЕМ? Примеры | МАТЕМАТИКА 5 классСкачать

Математика 5 Объем куба Соотношения между единицами объемаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Площадь поверхности куба. 5 кл.ЕГЭ(базовый уровень)Скачать
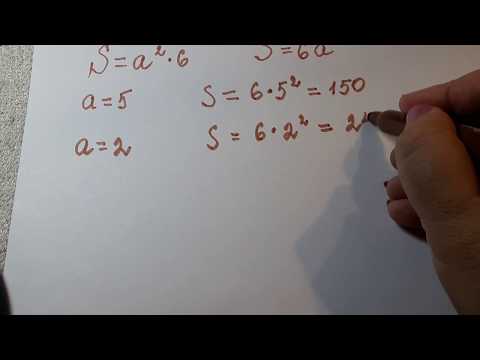
Многоугольники. 5 класс.Скачать

Площадь круга. Математика 6 класс.Скачать

Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать
