Как рассчитать 1 к 3 простой способ и подробное объяснение (7 видео)

Рассчитать отношение между двумя числами может быть достаточно просто, если знать основные правила и методы. Одним из наиболее распространенных типов отношений является отношение 1 к 3.

Для расчета отношения 1 к 3 нужно сначала понять, что такое отношение. Отношение – это способ сравнения двух чисел или величин, определяющий, сколько раз одно число (или величина) содержится в другом. В случае отношения 1 к 3, первое число (1) содержится второе число (3) один раз.

Чтобы рассчитать отношение 1 к 3, можно воспользоваться простым математическим выражением. Для этого нужно поделить второе число (3) на первое число (1). В результате получится отношение 3:1, что означает, что второе число в три раза больше первого.

Пример: Если у нас есть 3 яблока и мы хотим рассчитать отношение количества красных яблок к общему количеству яблок, то отношение будет равно 1 к 3 (1:3). Это означает, что из всех яблок одно будет красным, а остальные два будут другого цвета.

Содержание

Что такое дробь и как рассчитать её значение?
Определение дроби
Понятие числителя и знаменателя
Простое объяснение способа рассчета дроби
Как рассчитать 1 к 3 с помощью процента?
Определение процента
Решение задачи на проценты
Примеры применения процентного метода
Как рассчитать 1 к 3 с помощью деления?
Определение деления
Правила деления дробей
Примеры решения задач на деление
Как рассчитать 1 к 3 с помощью пропорции?
Определение пропорции
Правила пропорциональности
Примеры применения пропорций
Резюме
📹 Видео

Видео:Пропорция. Основное свойство пропорции. 6 класс.Скачать

Что такое дробь и как рассчитать её значение?

Расчет значения дроби осуществляется путем деления числителя на знаменатель. Например, чтобы рассчитать значение дроби 1/3, нужно разделить число 1 на число 3. После деления получится результат 0.33333333333…, в котором бесконечно повторяется цифра 3. Это происходит потому, что в десятичной системе чисел не все дроби можно представить конечным числом цифр.

Однако, для простых дробей, в которых знаменатель является степенью числа 10 (например, 10, 100, 1000 и т.д.), можно представить конечное число цифр после запятой. Например, чтобы рассчитать значение дроби 1/10, нужно разделить число 1 на число 10, что даст результат 0.1.

Таким образом, значение дроби может быть представлено в десятичном виде, как конечное число (например, 0.5) или как повторяющаяся десятичная дробь (например, 0.333333333…). Расчет значения дробей в математике является важным базовым навыком, который необходим для выполнения различных задач и операций.

Определение дроби

Например, в дроби 1/3 числитель равен 1, что означает, что мы берем только одну третью из целого. Знаменатель равен 3, что говорит нам о том, что мы имеем дело с третьями частями, разделенными на три равных части.

Дробная форма записи позволяет нам выразить обычные дроби, десятичные дроби и проценты. Например, 1/4 можно записать как 0.25 или как 25 процентов.

Важно понимать, что дроби — это не только числа, но и концепция в математике, используемая для представления частей целого.

Понятие числителя и знаменателя

Например, в дроби 1/3, числитель равен 1, что означает, что мы имеем одну часть целого числа. Знаменатель равен 3, что означает, что целое число разделено на три одинаковых части.

Числитель и знаменатель вместе позволяют нам определить значение дроби. В дроби 1/3, числитель определяет количество частей, а знаменатель определяет общее количество частей, на которые целое число разделено.

Интересный факт: В дроби 1/3, числитель и знаменатель могут быть увеличены или уменьшены на одно и то же число, и значение дроби останется неизменным. Например, если увеличить числитель и знаменатель на 2 (3/6), значение дроби все равно будет равно 1/3.

Важно понимать и использовать понятие числителя и знаменателя при рассчетах с дробями.

Простое объяснение способа рассчета дроби

Рассчет простых дробей может показаться сложным, но на самом деле это довольно простой процесс, если знать основные правила. Чтобы рассчитать дробь, у которой числитель равен 1, а знаменатель равен 3, нужно выполнить следующие шаги:

1. Понятие числителя и знаменателя:

Числитель — это число, которое находится сверху дроби. В нашем случае, числитель равен 1.

Знаменатель — это число, которое находится внизу дроби, под чертой. В нашем случае, знаменатель равен 3.

2. Рассчет дроби:

Чтобы рассчитать дробь, нужно числитель разделить на знаменатель. В нашем случае:

1 / 3 = 0.33 (округляем до двух знаков после запятой)

Примечание: рассчет можно выполнить как на обычном калькуляторе, так и при помощи программы для работы с математическими операциями.

3. Запись ответа:

Ответ записывается с использованием знака деления (/) и двух чисел — числителя и знаменателя. Так что наш ответ будет:

1 / 3 = 0.33

Исходя из вышеприведенных шагов, мы можем легко рассчитать дробь 1 к 3. Знание этих простых правил позволяет нам более точно и точно выполнять математические операции и делать расчеты.

Видео:МАТЕМАТИКА 6 класс: Отношения | ВидеоурокСкачать

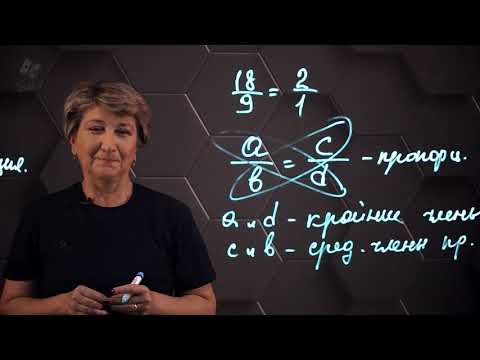
Как рассчитать 1 к 3 с помощью процента?

1 к 3 с помощью процента можно рассчитать следующим образом:

1 к 3
1	3

Для расчета процентного соотношения 1 к 3, необходимо разделить 1 на 3 и умножить на 100%. В результате получится соотношение 33,33% к 66,66%.

Пример:

У нас есть 100 предметов, и мы хотим разделить их в соотношении 1 к 3. Для этого:

Рассчитаем 33,33% от 100, получим 33,33 предмета.
Рассчитаем 66,66% от 100, получим 66,66 предмета.

Таким образом, в соотношении 1 к 3 из 100 предметов первому будет доставаться 33,33 предмета, а второму 66,66 предмета.

Расчет процентного соотношения 1 к 3 может быть полезен в различных ситуациях, например, при распределении ресурсов, определении долей участия в бизнесе или при разделении задач в команде.

Определение процента

Проценты широко используются во многих сферах, таких как финансы, экономика, статистика и торговля. Они позволяют выразить долю или отношение одного числа к другому в удобной форме.

Для определения процента необходимо знать два числа: числитель и знаменатель. Числитель представляет собой нужную нам долю или часть, а знаменатель — целое значение или общее количество.

Чтобы рассчитать процент, необходимо умножить числитель на 100 и разделить полученный результат на знаменатель. Полученное число будет являться искомым процентом.

Например, для расчета 20% от числа 100, необходимо выполнить следующие действия:

20 * 100 / 100 = 20

Таким образом, 20% от числа 100 составляет 20.

Использование процентов позволяет легко сравнивать различные значения и доли, а также делать прогнозы и анализировать данные.

Напоминаем, что процент — это всегда отношение, поэтому для полного понимания необходимо учитывать контекст и сравнивать его с другими значениями или долями.

Решение задачи на проценты

Для решения задачи на проценты необходимо следовать нескольким шагам. Рассмотрим пример: нужно рассчитать 20% от числа 150.

Шаг 1. Перевести процент в десятичную форму: 20% = 0,2.

Шаг 2. Умножить число на полученную десятичную долю: 150 * 0,2 = 30.

Ответ: 20% от числа 150 равно 30.

Таким образом, для решения задачи на проценты необходимо умножить число на десятичную долю от процента.

Примеры применения процентного метода

1. Расчет скидки. Если в магазине действует скидка в 30%, вы можете использовать процентный метод, чтобы быстро рассчитать сумму скидки на покупку. Например, если товар стоит 1000 рублей, то скидка составит 30% от этой суммы, то есть 300 рублей.

2. Расчет налога. Если вы хотите выяснить, сколько составляет налог от определенной суммы, процентный метод пригодится вам в этом случае. Например, если налоговая ставка составляет 15%, вы сможете легко рассчитать сумму налога, умножив исходную сумму на 0,15.

Исходная сумма	Налоговая ставка	Сумма налога
1000 рублей	15%	150 рублей
5000 рублей	10%	500 рублей

3. Расчет комиссии. Если вы осуществляете финансовые операции, такие как перевод денег посредством платежных систем, комиссия может быть рассчитана с помощью процентного метода. Например, если комиссия составляет 1,5% от переводимой суммы, вы сможете легко определить сумму комиссии, умножив исходную сумму на 0,015.

Таким образом, процентный метод может быть полезным инструментом в различных ситуациях, где требуется быстрый расчет процентных долей относительно исходных сумм. Он позволяет с легкостью определить сумму скидки, налога, комиссии и т. д.

Видео:ПРОПОРЦИЯ 6 класс математика отношения и пропорцииСкачать

Как рассчитать 1 к 3 с помощью деления?

Для того чтобы рассчитать 1 к 3 с помощью деления, нужно выполнить следующие шаги:

Шаг 1: Разложите число 1 на набор дробей с общим знаменателем 3. В данном случае, общим знаменателем будет число 3.

Шаг 2: Выполните деление числа 1 на число 3. Для этого разделите числитель дроби (1) на знаменатель дроби (3).

Шаг 3: Приведите получившуюся десятичную дробь к нужному виду. Например, можно округлить десятичную дробь до определенного количества знаков после запятой.

Итак, после выполнения этих шагов, вы получите результат 1 к 3 с помощью деления. Например, результат может быть равен 0,33333 или округлен до 0,33 в зависимости от указанной точности округления.

Определение деления

Чтобы выполнить деление, одно число делимых делим на другое число делителей. Чтобы указать деление, используется символ «/», который разделяет делимое и делитель. Например, для деления числа 10 на число 2, запись будет выглядеть как 10 / 2.

Результатом деления числа 10 на число 2 будет число 5, так как 10 делится на 2 ровно 5 раз. В данном случае, число 10 является делимым, число 2 — делителем, а число 5 — частным.

Деление можно рассматривать как противоположную операцию умножения. Вместо того, чтобы умножать одно число на другое, деление разделяет одно число на другое, чтобы определить, сколько раз одно число содержится в другом.

Деление имеет свои особенности и правила, которые необходимо учитывать при выполнении. Например, деление на ноль не определено в математике, так как невозможно разделить число на ноль.

Таким образом, деление — это основная математическая операция, которая позволяет разделить одно число на другое и определить, сколько раз одно число содержится в другом.

Правила деления дробей

1. Для деления дробей нужно умножить делимое на обратную дробь делителя.

Для того чтобы выполнить деление дробей, нужно домножить делимое на обратную дробь делителя. Обратная дробь получается путем замены числителя и знаменателя местами.

Например, чтобы рассчитать значение выражения 1/3 ÷ 2/5, нужно домножить делимое 1/3 на обратную дробь делителя 2/5. Таким образом, получается: (1/3) × (5/2) = 5/6.

2. Для деления дробей с одинаковым знаменателем, можно просто разделить числители.

Если у двух дробей одинаковый знаменатель, то результатом деления будет дробь с тем же знаменателем, а числитель получается путем деления числителя делимого на числитель делителя.

Например, чтобы рассчитать значение выражения 3/4 ÷ 2/4, можно просто разделить числители: (3/4) ÷ (2/4) = 3/2.

3. Если делитель – целое число, то деление сводится к умножению делимой дроби на обратное число делителя.

Если делитель является целым числом, то его можно представить в виде дроби с числителем равным этому числу и знаменателем равным 1. Деление тогда сводится к умножению делимой дроби на обратное число делителя.

Например, чтобы рассчитать значение выражения 2/3 ÷ 4, нужно домножить делимое 2/3 на обратное число делителя 1/4. Таким образом, получается: (2/3) × (1/4) = 2/12 = 1/6.

4. Для деления дробей с разными знаменателями, нужно привести дроби к общему знаменателю и затем разделить числители.

Если у двух дробей разные знаменатели, нужно привести их к общему знаменателю, а затем разделить числители полученных дробей.

Например, чтобы рассчитать значение выражения 1/3 ÷ 2/5, нужно привести обе дроби к общему знаменателю, который в данном случае будет равен 15 (наименьшее общее кратное чисел 3 и 5). Получаем: (1/3) ÷ (2/5) = (5/15) ÷ (6/15) = 5/6.

Правила деления дробей позволяют рассчитывать результаты деления дробей в разных случаях, их применение поможет вам с легкостью выполнять такие математические операции.

Примеры решения задач на деление

Ниже приведены несколько примеров задач на деление, чтобы прояснить процесс решения и показать, как можно использовать деление в повседневной жизни:

Пример 1: Разделите 18 на 3.

Решение:

18 делится на 3 без остатка 6 раз. Таким образом, ответ равен 6.

Пример 2: Какое число нужно разделить на 4, чтобы получить 16?

Решение:

Чтобы найти это число, мы можем использовать обратную операцию умножения. Мы умножим 4 на 16, чтобы получить 64. Таким образом, ответ равен 64.

Пример 3: На сколько частей нужно разделить пирог, чтобы каждый гость получил по 2 куска?

Решение:

Если каждый гость должен получить по 2 куска пирога, то мы должны разделить общее количество пирога на 2. Например, если у нас есть 8 кусков пирога, то мы можем разделить его на 2 и получить, что нам нужно разделить пирог на 4 части. Таким образом, ответ равен 4.

Это всего лишь несколько примеров задач на деление, и в реальности существует множество других ситуаций, когда деление может быть полезным. Важно понимать принцип деления и уметь применять его для решения различных задач.

Видео:Отношения - примеры и задачи. Математика 6 классСкачать

Как рассчитать 1 к 3 с помощью пропорции?

Для того чтобы рассчитать пропорцию, необходимо следовать нескольким шагам:

Записать пропорцию в виде уравнения: 1/x = 3/1, где «x» — неизвестная величина, которую мы хотим найти.
Умножить числитель одного отношения на знаменатель другого отношения: 1 * 1 = 3 * x
Решить полученное уравнение: 1 = 3x
Разделить обе части уравнения на коэффициент перед неизвестной величиной: x = 1/3

Таким образом, 1 к 3 равно 1/3. Это означает, что на каждую единицу первой величины приходится три единицы второй величины.

Определение пропорции

Пропорция имеет следующую структуру: a:b = c:d, где a, b, c и d — это числа или величины.

Анализ пропорции позволяет определить соотношение между частями целого или найти неизвестное значение в пропорции.

Существуют различные способы определения пропорции, одним из самых простых и понятных является способ «1 к 3». В этом способе задача состоит в нахождении третьего числа, если известны два числа и пропорция между ними.

Правила пропорциональности

Если у нас есть две пропорциональные величины A и B, то выполнены следующие правила:

1. Правило трех:

При пропорциональности трех величин A, B и C, отношение A к B равно отношению B к C.

То есть, если A пропорционально B, и B пропорционально C, то A пропорционально C.

2. Правило произведений:

Если две величины A и B пропорциональны, и одна из них умножается на число k, то другая величина тоже умножается на это число.

То есть, если A пропорционально B, то k * A пропорционально k * B.

3. Правило деления:

Если две величины A и B пропорциональны, и одна из них делится на число k, то другая величина тоже делится на это число.

То есть, если A пропорционально B, то A / k пропорционально B / k.

Используя эти правила пропорциональности, можно решать различные задачи, например, определение неизвестной величины, если известны пропорциональные величины.

Примеры применения пропорций

Пропорции могут быть полезными инструментами во многих сферах жизни. Рассмотрим несколько примеров, где пропорции могут применяться.

1. Кулинария:

При приготовлении пищи, важно соблюдать пропорции ингредиентов, чтобы получить оптимальный вкус. Например, в рецепте для пирога может быть указано, что необходимо использовать 1 чашку муки и 3 яйца. Это означает, что для каждой чашки муки нужно использовать 3 яйца, чтобы достичь желаемой текстуры и консистенции теста.

2. Фотография:

В фотографии пропорции могут использоваться для создания гармоничных композиций и равновесия. Например, правило третей (1 к 3) гласит, что изображение следует разделить на девять равных частей с помощью двух горизонтальных и двух вертикальных линий. Основные объекты или линии композиции затем размещаются вдоль этих линий или их пересечений, чтобы создать интересную визуальную динамику.

3. Архитектура:

Пропорции в архитектуре играют важную роль при создании устойчивых и эстетически приятных конструкций. Например, пропорции Золотого сечения, равные примерно 1:1,618, часто используются для определения соотношения размеров элементов здания. Это помогает создать гармоничное соотношение, которое приятно визуально воспринимать.

4. Моделирование:

В моделировании пропорции используются для создания точных и реалистичных моделей. Например, при создании модели автомобиля, важно соблюдать пропорции между его различными частями, чтобы модель выглядела правдоподобно и соответствовала оригиналу.

Все эти примеры демонстрируют важность пропорций в различных областях нашей жизни и как они могут быть использованы для достижения определенных целей и результатов.

Видео:Пропорции, 6 классСкачать

Резюме

В данной статье мы рассмотрели простой способ рассчитать 1 к 3 и дали подробное объяснение.

Прежде всего, мы уточнили, что 1 к 3 означает одну единицу на три части. Для расчета этого соотношения нужно разделить одну единицу на три и получить итоговую долю. Например, если у нас есть 1 кг сахара, то доля сахара будет составлять 1/3 кг или 333 г.

Мы также привели примеры других простых соотношений, таких как 1 к 2 и 1 к 4, и объяснили, как их рассчитать. Если есть необходимость выразить одну единицу в отношении к большему количеству или меньшему, то нужно просто поделить одну единицу на соответствующую часть соотношения.