Точки разрыва функции и их виды классификация и особенности (4 видео)

Точки разрыва функции – это особые точки на графике функции, где ее значения становятся неопределенными или бесконечными. В математике существуют несколько видов разрывов функций, каждый из которых имеет свои характеристики и особенности. Одним из важных аспектов изучения точек разрыва является классификация их видов, которая позволяет более полно осознать природу этих точек и их роль в функции.

Основные виды разрывов функций включают точки аналитического разрыва, точки скачка, устранимые точки разрыва и бесконечные точки разрыва. Точка аналитического разрыва – это точка, в которой функция разрывается, а ее значения могут быть определены только с помощью особых операций, таких как пределы или ряды. Точка скачка – это точка, где функция имеет разные значения с двух сторон и не может быть определена с помощью аналитических методов.

Устранимая точка разрыва – это особый вид разрыва, который можно устранить, изменяя или переопределяя функцию в окрестности этой точки. Однако, для этого требуется осуществить аналитические манипуляции с функцией. Бесконечная точка разрыва – это точка, в которой функция стремится к бесконечности или ее значения становятся бесконечно большими, разрываясь или образуя вертикальный асимптот.

Содержание

Раздел 1: Определение точки разрыва функции
Подраздел 1.1: Понятие точки разрыва
Подраздел 1.2: Основные характеристики точек разрыва
Раздел 2: Виды точек разрыва
Подраздел 2.1: Точки разрыва первого рода
Подраздел 2.2: Точки разрыва второго рода
Подраздел 2.3: Неразрывные точки
Раздел 3: Классификация точек разрыва
Подраздел 3.1: Точки разрыва удаленного значения
Подраздел 3.2: Точки разрыва промежуточного значения
Подраздел 3.3: Точки разрыва бесконечного значения
📺 Видео

Видео:Непрерывность функции и точки разрыва функцииСкачать

Раздел 1: Определение точки разрыва функции

Для определения точки разрыва функции необходимо рассмотреть её окрестность. Если существует два или более значений функции в пределах данной окрестности, то такая точка считается точкой разрыва.

Основные классификации точек разрыва функции включают:

Аналитические точки разрыва — точки, где функция имеет разрывы в своем аналитическом выражении. Это может быть, например, деление на ноль или нарастание функции до бесконечности.
Графические точки разрыва — точки, где функция имеет разрывы на графике, но не имеет аналитических разрывов. Это может произойти, например, при наличии пропуска значений функции или вертикальном разрыве графика.
Условные точки разрыва — точки, где функция имеет разрывы в силу определенных условий. Это может быть, например, переход функции на другую ветвь, изменение знака функции или непрерывное переключение между различными определениями функции.

Понимание и классификация точек разрыва функции играют важную роль в анализе функций и их свойств. Знание особенностей точек разрыва помогает в построении графиков, вычислении пределов и определении поведения функции в различных областях.

Подраздел 1.1: Понятие точки разрыва

Точки разрыва классифицируются на несколько видов в зависимости от свойств функции в данной точке:

Устранимые точки разрыва: в этом случае функция может быть непрерывной, если устранимый разрыв устранен.
Бесконечные точки разрыва: функция может стремиться к бесконечности или иметь полюс в данной точке.
Скачкообразные точки разрыва: график функции имеет разрыв, ограниченный значениями функции с разных сторон.
Гиперболические точки разрыва: функция стремится к бесконечности как положительной, так и отрицательной.

Каждый вид точки разрыва имеет свои особенности и может требовать различных подходов при анализе функции. Успешное исследование точек разрыва позволяет более полно понять поведение функции и выявить ее особенности.

Подраздел 1.2: Основные характеристики точек разрыва

Первый вид точек разрыва — точки разрыва первого рода или разрывы скачка. В этих точках значение функции с одной стороны отличается от значения с другой стороны. Например, функция может иметь разрыв при делении на ноль или при корне из отрицательного числа.

Второй вид точек разрыва — точки разрыва второго рода или разрывы устранимые. В этих точках функция может быть неопределена или иметь бесконечное значение, но это можно исправить путем определения функции или осуществления предельного перехода. Например, функция может иметь разрыв при делении на ноль, но если заменить значение точки разрыва пределом, то функция будет определена в этой точке.

Третий вид точек разрыва — точки разрыва третьего рода или разрывы разрывные. В этих точках не существует предела функции и она меняет свое поведение в окрестности разрыва. Например, функция может иметь разрыв, когда x стремится к некоторому значению, но значения функции стремятся к двум разным числам.

Точки разрыва первого рода характеризуются различными значениями функции с разных сторон.
Точки разрыва второго рода характеризуются неопределенностью или бесконечными значениями функции.
Точки разрыва третьего рода характеризуются отсутствием предела функции и ее изменением в окрестности разрыва.

Основные характеристики точек разрыва зависят от их вида и могут быть использованы для анализа поведения функции в окрестности этих точек.

Видео:Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Раздел 2: Виды точек разрыва

Точки разрыва функции могут иметь различные виды в зависимости от своего поведения в окрестности. Рассмотрим основные классификации точек разрыва:

Существенные точки разрыва:

Это точки, в которых функция не имеет предела ни справа, ни слева. В окрестности таких точек функция может иметь разные значения или она может вообще не существовать.

Устранимые точки разрыва:

Это точки, в которых функция может иметь разрыв, но этот разрыв может быть «устранен» путем определения значения функции в этой точке. Например, если функция не определена в некоторой точке, но значение, к которому она стремится, можно задать непрерывностью, то такая точка будет устранимой точкой разрыва.

Полюса:

Это точки, в которых функция имеет бесконечно увеличивающиеся или убывающие значения. В окрестности таких точек функция может стремиться к бесконечности.

Каждый из этих видов точек разрыва имеет свои особенности и может вносить определенные изменения в график функции. При изучении точек разрыва рекомендуется учитывать их вид, чтобы корректно анализировать и описывать поведение функции.

Подраздел 2.1: Точки разрыва первого рода

Точки разрыва первого рода характеризуются тем, что в них функция либо не определена, либо определена, но имеет разные значения слева и справа от данной точки. Это означает, что функция имеет разрыв на графике.

Существует несколько типов точек разрыва первого рода:

Устранимый разрыв: в этом случае функция определена на некотором интервале, но имеет разрыв в одной или нескольких точках. В этих точках функцию можно доопределить таким образом, чтобы она стала непрерывной.
Бесконечный разрыв: в данной точке функция не определена и её значение стремится к бесконечности. Это может происходить, например, когда в знаменателе функции присутствует нуль.
Разрыв скачка: функция определена как слева, так и справа от данной точки, но значения функции различаются. При движении по графику в одном направлении функция может иметь различные значения до и после точки разрыва.

Точки разрыва первого рода играют важную роль в анализе функций. Они могут встречаться в различных математических задачах и представлять особые точки, на которых функция обнаруживает необычное поведение.

Подраздел 2.2: Точки разрыва второго рода

Точки разрыва второго рода классифицируются на следующие типы:

Устранимый разрыв: в этом случае, предел функции в точке разрыва существует, но значение функции в этой точке отсутствует или некорректно определено. Устранимый разрыв может возникать, например, при делении на ноль в знаменателе функции.
Бесконечный разрыв: в этом случае, предел функции в точке разрыва существует, но его значение равно бесконечности. Бесконечный разрыв может возникать, например, при делении положительной константы на ноль или при извлечении корня из отрицательного числа.

Важно отметить, что точки разрыва второго рода не являются точками неопределенности функции, так как в них определен предел функции. Однако, значения функции в этих точках могут быть некорректными или бесконечными.

Подраздел 2.3: Неразрывные точки

Особенность неразрывных точек заключается в том, что функция может быть гладкой и непрерывной в области около такой точки. Такие точки могут быть крайне полезны, особенно при решении задач и оптимизации функций.

Чтобы определить, является ли точка разрывной или неразрывной, необходимо изучить пределы функции с обоих сторон от данной точки. Если предел существует и совпадает с значением функции в этой точке, то она является неразрывной. Если пределы с обеих сторон не существуют или не совпадают, то точка является разрывной.

Неразрывные точки обладают важными свойствами, такими как непрерывность функции и возможность дифференцирования. Они играют важную роль в анализе функций и позволяют более точно определить их характеристики и поведение.

Понимание неразрывных точек и их классификация помогает улучшить понимание функций и их свойств. Изучение и анализ таких точек является одной из ключевых тем в математике и приложениях к ней.

Видео:Математический анализ, 5 урок, Непрерывность функцииСкачать

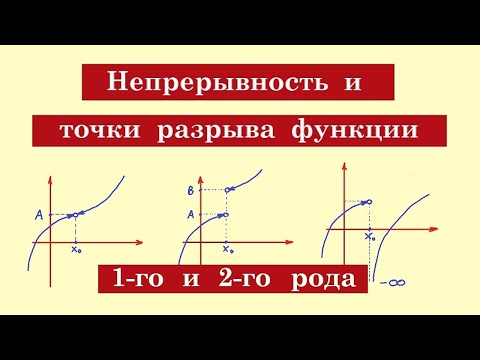
Раздел 3: Классификация точек разрыва

Точки разрыва функции могут быть классифицированы по различным критериям, отражающим их особенности. В этом разделе рассмотрим основные виды точек разрыва и их классификацию.

Вид разрыва	Описание
Существенный разрыв	В данной точке функция не имеет предела или предел функции бесконечен. Это может происходить, например, когда функция имеет разные значения при приближении к точке с разных сторон.
Устранимый разрыв	В данной точке функция имеет разрыв, но предел функции существует. Разрыв является «устраняемым» в том смысле, что если определить функцию в этой точке заново, то она будет непрерывной.
Разрыв первого рода	В данной точке функция имеет разные односторонние пределы существующие с разных сторон. Это означает, что значение функции в этой точке не является определенным.
Разрыв второго рода	В данной точке функция не имеет ни одного одностороннего предела. Это может происходить, например, когда функция имеет разные значения при приближении к точке с разных сторон, но и ни одно из этих значений не является пределом функции.

Классификация точек разрыва позволяет более детально изучить поведение функции вблизи этих точек и применять соответствующие методы анализа функций. Знание видов точек разрыва и их особенностей является важной частью математического анализа и позволяет более глубоко понять свойства функций.

Подраздел 3.1: Точки разрыва удаленного значения

Точка разрыва удаленного значения может быть классифицирована как полюс (когда функция стремится к бесконечности без ограничения) или изолированная точка разрыва (когда функция принимает значение, которое отличается от остальных значений функции вблизи данной точки).

Особенностью точек разрыва удаленного значения является то, что они требуют особых подходов при анализе функций. В частности, для точек разрыва удаленного значения не может быть определен лимит функции в данной точке, так как функция не имеет ограниченного значения. Кроме того, при работе с такими точками, требуется учитывать их классификацию (полюс или изолированная точка разрыва), чтобы определить особенности их поведения.

Изучение точек разрыва удаленного значения в функциях играет важную роль в математике и физике, так как позволяет определить границы применимости функций, а также выявлять их специфические свойства и поведение в окрестности данных точек.

Подраздел 3.2: Точки разрыва промежуточного значения

Точки разрыва промежуточного значения возникают, когда функция имеет неопределенные значения в каких-то определенных точках. Это означает, что функция может не иметь значения в этих точках или иметь разные значения при приближении к ним с разных сторон.

Промежуточные точки разрыва бывают двух видов: скачки и разрывы.

Скачок в функции происходит, когда функция имеет разные значения при приближении к точке с разных сторон. Например, функция может иметь значение 1 при x < 0 и значение -1 при x >= 0. В таком случае, точка x = 0 будет точкой скачка.

Разрыв в функции возникает, когда функция не имеет значения в определенной точке. Это может происходить, когда функция имеет разные определения на интервалах, около которых находится эта точка. Например, функция может быть определена как x^2 при x < 0 и как sqrt(x) при x >= 0. В таком случае, точка x = 0 будет точкой разрыва.

Точки разрыва промежуточного значения являются особыми точками в функции и могут создавать различные проблемы при анализе функции и решении уравнений. Поэтому, при работе с функциями, важно учитывать и анализировать точки разрыва промежуточного значения.

Подраздел 3.3: Точки разрыва бесконечного значения

В функциях также могут существовать точки разрыва бесконечного значения. Здесь функция не может быть определена в некоторой точке из-за дивергенции ее значения к бесконечности.

Точку разрыва бесконечного значения можно классифицировать на два основных типа: точки разрыва первого рода и точки разрыва второго рода.

Точка разрыва первого рода возникает, если пределы функции с разных сторон от этой точки бесконечны, но эти пределы сами не бесконечны.

Точка разрыва второго рода возникает, когда пределы функции с разных сторон от этой точки бесконечны, и хотя бы один из них является бесконечным пределом.

Особенность точек разрыва бесконечного значения заключается в том, что в окрестности такой точки функция стремится к бесконечности, и поэтому она не имеет определенного значения.