Одной из важных задач в машинном обучении является классификация данных. Данная задача заключается в разделении набора данных на категории или классы в соответствии с определенными критериями. В зависимости от характера данных и цели исследования, для классификации могут быть применены различные подходы. Для решения задачи классификации важно выбрать подходящий тип классификации, который позволит достичь наилучших результатов.
Один из типов классификации, который подходит для динамической модели, — это метод временных рядов. Временной ряд представляет собой последовательность значений, измеренных в разные моменты времени. Динамическая модель, в свою очередь, описывает эволюцию системы со временем. При использовании метода временных рядов для классификации динамической модели, основной упор делается на анализ временных зависимостей и закономерностей в данных. Такой подход может быть полезен, например, при прогнозировании временного ряда или определении временного интервала, в течение которого произойдет определенное событие или изменение.
Для применения метода временных рядов в классификации необходимо провести предварительный анализ данных и выделить основные компоненты временного ряда, такие как тренд, сезонные колебания, циклические и случайные факторы. Затем можно приступить к выбору подходящего алгоритма классификации, который будет учитывать эти компоненты и позволит достичь наилучшего результата. В процессе классификации можно использовать различные модели временных рядов, такие как арима, авторегрессия или экспоненциальное сглаживание. Кроме того, для повышения точности классификации можно применять различные методы прогнозирования и анализировать дополнительные признаки, такие как погодные данные или данные социологических опросов.
- Динамическая модель: классификация и ее типы
- Что такое динамическая модель и почему она важна?
- Значение и применение динамических моделей в науке и инженерии
- Виды классификации моделей
- Статическая и динамическая классификация в инженерии
- Классификация моделей по уровню детализации
- Свойства динамических моделей и их классификация
- Линейные и нелинейные динамические модели
- Физические и математические динамические модели
- Выбор типа классификации для динамической модели
- Особенности и требования к модели и проекту
- Преимущества и недостатки различных типов классификации
- Рекомендации по выбору типа классификации в конкретных задачах
- Примеры применения различных типов классификации в инженерии
- 🌟 Видео
Видео:Обучение модели и оценка качества классификацииСкачать

Динамическая модель: классификация и ее типы
Существует несколько типов классификации динамических моделей:
- Линейные модели: такие модели описываются линейными дифференциальными уравнениями. Они хорошо подходят для систем с линейными зависимостями и малым числом параметров. Примером может служить модель движения математического маятника.
- Нелинейные модели: описываются нелинейными дифференциальными уравнениями. Они предназначены для сложных систем, где имеются нелинейные зависимости между переменными.
- Стохастические модели: такие модели учитывают случайные факторы. Они применяются в задачах прогнозирования, где важна вероятностная оценка изменений в системе.
- Рекуррентные модели: используются для описания систем, где текущее состояние зависит от предыдущих состояний. Они позволяют учесть исторические данные и предсказать будущее поведение системы.
- Дискретные модели: описывают системы, в которых изменения происходят дискретно по времени. Такие модели встречаются, например, в теории автоматов и дискретных событийных системах.
Выбор типа классификации динамической модели зависит от требований и характера изучаемой системы. Важно учитывать особенности моделируемой системы, доступность и достоверность данных, а также необходимость предсказания будущего состояния системы. Каждый тип модели имеет свои преимущества и ограничения, и выбор оптимального типа является ключевым фактором для достижения точности и релевантности результатов моделирования.
Видео:КЛАССИФИКАЦИЯ В МАШИННОМ ОБУЧЕНИИ на Python. ТОП-7 АЛГОРИТМОВ КЛАССИФИКАЦИИ на Практике!Скачать

Что такое динамическая модель и почему она важна?
Динамическая модель может быть представлена в виде дифференциальных уравнений, разностных уравнений или системы уравнений. Она позволяет описать, предсказать и анализировать различные аспекты поведения системы, такие как изменение ее состояния, воздействие внешних факторов, переходы между состояниями и динамику изменения параметров.
Важность динамической модели заключается в возможности более точного и полного описания системы, а также в предсказании ее поведения в будущем. Она позволяет провести различные сценарные анализы и эксперименты, оценить воздействие различных переменных и факторов на систему, и принять обоснованные решения на основе полученных результатов.
Благодаря динамической модели можно проанализировать, как изменятся параметры системы при изменении внешних условий, каковы будут долгосрочные тенденции и как будет вести себя система в кризисных ситуациях. Также динамическая модель позволяет определить оптимальные стратегии управления и прогнозировать последствия различных решений.
Использование динамических моделей особенно важно в таких областях, как физика, экономика, биология, метеорология, управление производством и финансами. Они позволяют лучше понять и предсказать поведение сложных систем, а также оптимизировать и усовершенствовать процессы управления и принятия решений.
Значение и применение динамических моделей в науке и инженерии
Динамические модели играют важную роль в различных областях науки и инженерии. Они позволяют описать и предсказать поведение сложных систем во времени, учитывая взаимодействия между их компонентами и изменения внешних условий.
Одним из основных применений динамических моделей является исследование и оптимизация процессов в различных областях науки, таких как физика, химия и биология. Например, моделирование динамики химических реакций позволяет предсказать характеристики исходных и конечных веществ, что является важным при проектировании новых материалов и лекарств. В биологии динамические модели применяются для изучения эволюции популяций и взаимодействия вида с окружающей средой.
Динамические модели также находят широкое применение в инженерии. Проектирование и оптимизация сложных систем, таких как автомобили, самолеты и энергетические установки, требует предварительного анализа и моделирования их динамического поведения. Моделирование включает описание движения, текучести и электрического или механического взаимодействия компонентов системы.
Одной из особенностей динамических моделей является их способность предсказывать будущие состояния системы на основе начальных условий и входных параметров. Это позволяет прогнозировать результаты изменений в системе и заранее принимать необходимые меры для достижения желаемого результата.
Таким образом, динамические модели являются эффективным инструментом для исследования и оптимизации сложных систем в науке и инженерии. Они позволяют улучшить процессы проектирования, прогнозирования и принятия решений, что способствует развитию научных и технических отраслей и содействует прогрессу человечества в целом.
Видео:Персептрон - возможности классификации образов, задача XOR | #2 нейросети на PythonСкачать

Виды классификации моделей
Существует несколько видов классификации моделей, которые могут быть использованы при создании динамической модели:
- Бинарная классификация — моделирование, в котором объекты классифицируются только на два класса. Например, можно классифицировать письма как спам или не спам.
- Многоклассовая классификация — моделирование, в котором объекты классифицируются на несколько классов. Например, можно классифицировать изображения на категории животных.
- Последовательная классификация — моделирование, в котором объекты классифицируются последовательно по нескольким классам. Например, можно классифицировать текст на основе его содержания и стиля.
- Иерархическая классификация — моделирование, в котором объекты классифицируются согласно иерархической структуре классов. Например, можно классифицировать товары на основе их категорий и подкатегорий.
Выбор подходящего типа классификации модели зависит от цели и задачи, которую необходимо решить.
Статическая и динамическая классификация в инженерии
Статическая классификация применяется для статичных объектов или систем, где характеристики объекта не меняются со временем. Она основана на разделении объектов на классы или категории в соответствии с определенными признаками или характеристиками. Например, в архитектуре можно классифицировать здания по их типу (жилые, офисные, промышленные) или по стилю (классический, модерн, современный).
Динамическая классификация применяется для объектов или систем, в которых характеристики могут меняться со временем. Она учитывает динамику изменений и позволяет классифицировать объекты или процессы в зависимости от их состояния или эволюции. Например, в автопроме можно классифицировать транспортные средства по типу движения (городской, загородный, специализированный) и учитывать их примерное расходование топлива или нормы износа.
Выбор между статической и динамической классификацией зависит от особенностей объекта или системы, а также от цели классификации. В некоторых случаях можно сочетать оба подхода, что позволит получить более полную и точную картину. Например, при классификации компьютерных систем можно учитывать их статические параметры (тип процессора, объем памяти) и динамические характеристики (скорость работы, энергопотребление).
В итоге, статическая и динамическая классификация в инженерии играют важную роль в систематизации и описании объектов и процессов. Выбор между ними зависит от характера модели и данных, а также от целей и задач классификации. Эффективное использование обоих подходов позволяет получить более точное представление о системе и сделать правильные инженерные решения.
Классификация моделей по уровню детализации
Модели могут быть классифицированы как простые, средней сложности и сложные. Простые модели являются наиболее общими и обладают минимальным уровнем детализации. Они часто используются для простых задач классификации, когда требуется быстрый и простой анализ данных. Примерами простых моделей могут быть логистическая регрессия или наивный Байесовский классификатор.
Модели средней сложности обладают более высоким уровнем детализации и учитывают больше факторов при классификации данных. Они могут использоваться для более сложных задач и предоставляют более точные результаты. Примерами средних моделей могут быть деревья решений или метод опорных векторов.
Сложные модели являются наиболее детализированными и обладают высочайшим уровнем сложности. Они могут использоваться для сложных задач классификации, когда требуется учитывать большое количество факторов и осуществлять более точный анализ данных. Примерами сложных моделей могут быть нейросети или глубокое обучение.
Выбор модели зависит от множества факторов, включая тип данных, размер выборки, доступные вычислительные ресурсы и требуемую точность классификации. При выборе модели необходимо учитывать баланс между уровнем детализации и вычислительной сложностью, чтобы достичь оптимальных результатов.
Видео:Строим Нейронную Сеть для Распознавания Изображений за 20 минутСкачать

Свойства динамических моделей и их классификация
Одним из свойств динамических моделей является возможность учета изменения состояния системы с течением времени. В отличие от статических моделей, которые описывают систему в один момент времени, динамические модели представляют собой набор уравнений, которые описывают изменение состояния системы в течение времени.
Еще одним свойством динамических моделей является наличие временной компоненты. Динамические модели учитывают не только текущее состояние системы, но и предсказывают, как это состояние может измениться в будущем. Это позволяет прогнозировать поведение системы и осуществлять управление ею.
В зависимости от поведения системы динамические модели можно разделить на несколько типов:
- Линейные модели: описывают системы, которые могут быть представлены линейными уравнениями. Такие модели находят широкое применение в системах автоматического управления.
- Нелинейные модели: описывают системы, которые могут быть представлены нелинейными уравнениями. Такие модели используются, когда поведение системы не может быть описано линейными зависимостями.
- Дискретные модели: описывают системы, которые изменяют свое состояние только в дискретные моменты времени. Такие модели используются, например, в теории игр и теории управления.
- Непрерывные модели: описывают системы, которые изменяют свое состояние непрерывно во времени. Такие модели широко применяются в физике, химии и биологии.
Классификация динамических моделей позволяет более точно определить их свойства и применение. Выбор конкретного типа модели зависит от требований и особенностей исследуемой системы.
Линейные и нелинейные динамические модели
Для построения динамической модели необходимо выбрать подходящий тип классификации. В этом контексте особенно важно различать два основных типа моделей: линейные и нелинейные.
Линейные динамические модели характеризуются линейной зависимостью между входными и выходными данными. Они обладают простой структурой и удобны для анализа, но могут быть ограничены в точности предсказаний. Линейные модели хорошо работают в случае, когда система подчиняется линейным законам и не имеет сложных нелинейных взаимодействий.
Нелинейные динамические модели, напротив, могут учитывать более сложные зависимости между входными и выходными данными. Они позволяют моделировать нелинейные эффекты, такие как неоднородность, взаимодействия между различными переменными и нелинейные трансформации данных. Нелинейные модели являются более гибкими, но требуют более сложных алгоритмов обучения и анализа.
Выбор между линейными и нелинейными динамическими моделями зависит от специфики задачи и доступных данных. Если имеются явные линейные закономерности и простота модели важнее точности предсказания, то линейные модели могут быть предпочтительнее. Если же необходимо учитывать сложные взаимодействия между переменными и достичь более точных предсказаний, то нелинейные модели являются более подходящим выбором.
Физические и математические динамические модели
Физическая модель основывается на фундаментальных законах природы и позволяет более полно и точно описывать системы. Она учитывает реальные физические параметры и характеристики, такие как масса, скорость, сила и т.д. Однако создание физической модели требует больших затрат времени и ресурсов, а также точного знания физических принципов и уравнений. Кроме того, физические модели могут быть сложными и трудно поддающимися анализу.
Математическая модель, в свою очередь, использует математические уравнения и алгоритмы для описания системы. Она может быть простой и понятной для анализа, что делает ее более удобной в применении. Математические модели обычно требуют меньше времени и ресурсов для создания и могут быть сконструированы даже без глубоких знаний в физике. Однако математические модели могут не учитывать некоторые реалии реального мира или упрощать систему, что может привести к неточным результатам и пропускам некоторых факторов.
В идеале, при решении задач динамического моделирования следует использовать сочетание физических и математических моделей. Это позволит получить более точные и реалистичные результаты, учитывая и физические особенности системы, и ее математическое описание. Такой подход позволяет создавать более надежные и эффективные системы управления и строить прогнозы, основанные на точных и обоснованных моделях.
| Физические модели | Математические модели |
|---|---|
| Основываются на фундаментальных законах природы | Используют математические уравнения и алгоритмы |
| Точное описание системы | Простота и понятность для анализа |
| Требуют больших затрат времени и ресурсов | Требуют меньше времени и ресурсов |
| Сложны и трудно поддаются анализу | Могут не учитывать некоторые реалии реального мира |
В итоге, выбор между физической и математической моделью зависит от конкретной задачи и доступных ресурсов. Использование сочетания обоих типов моделей позволяет получить наилучший результат и более точные прогнозы.
Видео:Моделирование как метод познания | Информатика 9 класс #5 | ИнфоурокСкачать

Выбор типа классификации для динамической модели
При разработке динамических моделей, которые должны адаптироваться к изменяющимся условиям и обновляться в режиме реального времени, важно выбрать подходящий тип классификации. Тип классификации определяет способ группировки данных и присвоения им меток, а также алгоритмы и модели, используемые для этого.
В контексте динамической модели часто используется инкрементальная классификация. При инкрементальной классификации модель обучается на новых данных, поступающих в реальном времени, и обновляется без переобучения на всем наборе данных. Такой подход позволяет модели динамично адаптироваться к изменяющимся условиям и предсказывать результаты более точно.
Для инкрементальной классификации может использоваться различный набор алгоритмов, таких как алгоритмы наивного Байеса, методы опорных векторов (SVM), деревья решений и многие другие. Каждый из этих алгоритмов имеет свои особенности и применим для разных типов данных и задач.
Для выбора подходящего типа классификации для динамической модели необходимо учитывать как специфику данных, так и требования к точности и скорости работы модели. Важно также учесть возможность обновления модели и наличие возможности объединения данных из разных источников.
Кроме того, для успешной классификации в динамической модели необходимо применять методы обработки и предварительного анализа данных. Это может включать в себя нормализацию и шкалирование данных, обнаружение и удаление выбросов, а также преобразование признаков для улучшения качества классификации.
Наконец, необходимо учитывать возможность применения ансамблевых моделей. Ансамблевый метод объединяет несколько моделей вместе для улучшения точности классификации. Такие модели могут быть полезны в случае динамической модели, так как они могут обнаруживать и приспосабливаться к изменениям в данных с большей точностью.
Выбор типа классификации для динамической модели играет важную роль в успешном адаптировании модели к изменяющимся условиям и обеспечении точности предсказаний. Необходимо учитывать требования и специфику данных, применять методы обработки данных и ансамблевые модели для улучшения качества классификации.
Особенности и требования к модели и проекту
При создании динамической модели классификации необходимо учитывать ряд особенностей и требований, которые помогут достичь оптимальных результатов и эффективно применить модель в проекте.
- Актуальность данных. Для динамической модели необходимо иметь постоянный доступ к актуальным данным, поскольку они могут быстро меняться.
- Учет динамической природы данных. Динамическая модель должна учитывать изменения в данных и способность быстро адаптироваться к новым условиям.
- Масштабируемость. Модель должна быть способна обрабатывать большой объем данных и эффективно работать с различными входными параметрами.
- Устойчивость к выбросам. Динамическая модель должна быть устойчива к случайным выбросам или отклонениям в данных.
- Простота использования. Модель должна быть понятной и легко внедряемой в проект, чтобы пользователи могли с легкостью работать с ней.
- Высокая точность. Модель должна давать высокую точность предсказаний и классификации для различных типов данных.
- Быстрая скорость обработки. При работе с динамическими данными важна быстрота обработки, поскольку реальное время может быть критическим фактором.
Учитывая эти особенности и требования, можно выбрать подходящий тип классификации для динамической модели и успешно применить ее в проекте.
Преимущества и недостатки различных типов классификации
1. Логистическая регрессия
Преимущества:
- Простота и легкость интерпретации модели;
- Хорошо работает с малым набором данных;
- Модель позволяет оценить вероятности принадлежности к классам, а не только классифицировать данные.
Недостатки:
- Плохо работает в случае сложных нелинейных зависимостей;
- Неустойчивость к выбросам и отсутствию линейности в данных;
- Низкая точность классификации в задачах с большим количеством классов.
2. Деревья принятия решений
Преимущества:
- Легко интерпретируемы и понятны для человека;
- Обработка больших объемов данных за короткое время;
- Могут работать с данными разного типа (категориальные и числовые переменные).
Недостатки:
- Склонность к переобучению;
- Сложность работы с непрерывными данными;
- Чувствительность к изменениям в данных.
3. Метод опорных векторов
Преимущества:
- Устойчивость к выбросам и шумам в данных;
- Модель эффективна в задачах с большим количеством признаков;
- Может работать с линейно неразделимыми данными благодаря использованию ядерных функций.
Недостатки:
- Требуется настройка параметров модели;
- Модель может быть очень взрывоопасной и неустойчивой при неправильном выборе ядра;
- Модель может быть медленной в обучении для больших объемов данных.
4. Нейронные сети
Преимущества:
- Могут обрабатывать сложные нелинейные зависимости;
- Могут работать с данными разного типа;
- Высокая точность и производительность при правильной настройке модели и большом объеме данных.
Недостатки:
- Требуют большого количества обучающих данных для эффективной работы;
- Требуют много ресурсов для обучения и работы модели;
- Чувствительность к выбору гиперпараметров и их настройке.
Видео:12.2 Метод ближайших соседей - KNNСкачать
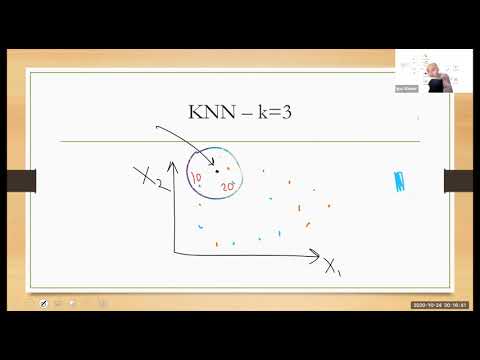
Рекомендации по выбору типа классификации в конкретных задачах
1. Бинарная классификация: Если задача заключается в разделении объектов на два класса, например, определение, является ли письмо спамом или нет, то бинарная классификация является подходящим выбором.
2. Многоклассовая классификация: Если требуется классификация объектов на несколько классов, например, определение языка текста или распознавание рукописных цифр, следует использовать многоклассовую классификацию.
3. Динамическая классификация: Если задача имеет динамическую природу и требует учета изменений в данных с течением времени, то подходящим выбором может быть динамическая классификация. Например, в задачах прогнозирования финансовых рынков или анализа потребительского поведения, когда данные постоянно обновляются и изменяются, динамическая модель классификации может быть эффективной.
4. Нелинейная классификация: В случаях, когда существует нелинейная зависимость между признаками и целевой переменной, следует рассмотреть использование нелинейных моделей классификации, например, нейронных сетей или методов, основанных на деревьях решений.
5. Вероятностная классификация: Если важно получить вероятности принадлежности объектов к различным классам, например, в задачах ранжирования или оценки уверенности модели, следует использовать вероятностные модели классификации, такие как наивный байесовский классификатор или логистическая регрессия.
Примеры применения различных типов классификации в инженерии
Логистическая регрессия
Логистическая регрессия — это один из наиболее распространенных методов классификации в инженерии. Она используется, когда нужно разделить данные на два класса. Например, логистическая регрессия может быть применена для определения, является ли изделие дефектным или нет на основе набора характеристик или признаков.
Метод опорных векторов
Метод опорных векторов (SVM) широко используется для классификации в инженерии, особенно когда данные нелинейно разделимы. Например, SVM может быть применен для определения типа повреждений на поверхности металла по набору сигналов, полученных с помощью датчиков. SVM позволяет создавать разделительные гиперплоскости для эффективного разделения данных.
Деревья решений
Деревья решений являются гибким инструментом классификации в инженерии. Они могут быть использованы для решения различных задач классификации, включая определение дефектов в структурах, прогнозирование надежности систем, анализ и идентификацию сигналов и многое другое. Деревья решений позволяют представлять данные в виде дерева, где каждый узел представляет характеристику, а каждое листовое значение соответствует конечному классу объекта.
Случайный лес
Случайный лес — это ансамбль деревьев решений, который может быть использован для классификации в инженерии. Случайный лес может работать с большими объемами данных и имеет высокую степень устойчивости к шуму. Он может быть применен для решения задач классификации, таких как определение типа повреждений в строительных материалах, анализ причин отказов и прогнозирование прочности структур.
Нейронные сети
Нейронные сети — это мощный инструмент классификации в инженерии, который может использоваться для обработки различных типов данных. Нейронные сети могут быть применены для решения сложных задач классификации, таких как определение типа дефектов на изображениях, анализ временных рядов и обработка сигналов.
Примечание: Данные примеры показывают только некоторые из возможных применений различных типов классификации в инженерии. Реальные применения могут быть гораздо более широкими и разнообразными.
🌟 Видео
Основные Типы Современных Баз Данных Которые Используются в ПрактикеСкачать

Лекция 15. КлассификацияСкачать

Статистический метод (критерий): как выбрать для анализа?Скачать

Занятие 4. Семинар. Классификация текстов. Предобученные модели и huggingface.Скачать

089. Мастер класс Решение задач классификации при помощи CatBoost – Никита ДмитриевСкачать

8 преимуществ сводной по Модели Данных в ExcelСкачать

Разновидности архитектур нейросетей | НЕЙРОСЕТЬ ИЗНУТРИСкачать

Топ 3 худших программиста на YouTube! #код #айти #программистСкачать

Pydantic — умопомрачительная валидация данных на Python! JSON + Pydantic = ❤️Скачать

Что такое NoSQL за 6 минутСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Мода, размах, среднее арифметическое, медианаСкачать

Что такое API?Скачать

Лекция. Генерация текста с помощью языковых моделейСкачать
