Для принятия решений важно уметь анализировать показатели и находить оптимальные решения. Одним из инструментов такого анализа является средняя гармоническая невзвешенная альтернатива, которая позволяет учитывать различные факторы и дает более точную оценку.
Средняя гармоническая невзвешенная альтернатива используется для расчета среднего значения нескольких чисел. Она отличается от средней арифметической невзвешенной тем, что при обработке данных учитывается их взаимосвязь и весовые коэффициенты, что делает её более точной и полезной.
Среднюю гармоническую невзвешенную альтернативу можно вычислить по формуле, которая учитывает все значения и их весовые коэффициенты. Такой подход использовался в финансовых расчетах, медицинских исследованиях, анализе рынка и других областях, где важна точность и объективность оценок.
Видео:Средняя арифметическая и гармоническая. Примеры.Скачать

Что такое средняя гармоническая невзвешенная?
Средняя гармоническая невзвешенная вычисляется по формуле:
H = N / (1/X1 + 1/X2 + … + 1/Xn)
Где X1, X2, …, Xn — значения величин, N — количество значений.
Основное применение средней гармонической невзвешенной заключается в случаях, когда нужно учесть обратную пропорциональность между значениями. Например, она широко используется при расчете средней скорости движения, когда время и расстояние обратно пропорциональны.
Средняя гармоническая невзвешенная имеет несколько преимуществ. Во-первых, она предоставляет среднее значение, которое ближе к минимальным значениям величин, чем средняя арифметическая. Во-вторых, она подходит для использования с наборами данных, в которых значения имеют обратную пропорцию друг с другом.
Важно отметить, что средняя гармоническая невзвешенная может быть менее устойчивой к выбросам или экстремальным значениям, чем другие методы вычисления среднего значения. Поэтому перед использованием этого показателя необходимо внимательно изучить данные и учесть особенности конкретной ситуации.
Видео:Средние величины - арифметическая и гармоническая взвешенныеСкачать

Принцип работы средней гармонической невзвешенной
Принцип работы средней гармонической невзвешенной заключается в следующем. Для начала, каждое число в наборе возводится в степень -1. Затем, полученные значения складываются. И, наконец, сумма этих значений делится на общее количество чисел в наборе. Результатом будет среднее гармоническое невзвешенное данного набора чисел.
Средняя гармоническая невзвешенная является особенным методом расчета среднего значения, поскольку она учитывает пропорциональное влияние каждого числа в наборе. Это особенно полезно, когда имеется набор чисел, где каждое число представляет собой какую-то степень или отношение к другому числу.
Преимуществом средней гармонической невзвешенной является ее учет влияния экстремальных значений. Даже небольшие значения в наборе могут оказывать значительное влияние на итоговое среднее, что позволяет учесть потенциальные выбросы в данных.
Однако следует отметить, что применение средней гармонической невзвешенной требует осторожности. Она может быть более чувствительной к выбросам и аномалиям по сравнению с другими методами расчета среднего значения. Также важно использовать этот метод с учетом особенностей конкретной задачи или области применения.
Сравнение средней гармонической невзвешенной и средней арифметической невзвешенной
СГН используется, когда нужно учесть инверсию отношений или пропорций между значениями данных. Этот метод является более устойчивым к выбросам и выборкам с неравномерными значениями. СГН может быть полезна, например, при измерении скорости или силы, так как она воспринимает инверсию значений более точно.
САН является самым простым методом вычисления среднего значения. Он подходит для равномерных данных без инверсий и отношений, и в большинстве случаев дает достаточно точный результат. Такой метод часто используется в экономике, статистике и других областях, где нет необходимости учитывать пропорции и инверсии.
При сравнении СГН и САН необходимо учитывать свойства данных и цели исследования. Если инверсии или пропорции играют важную роль, то СГН будет предпочтительнее. В случае равномерных данных без инверсий САН можно использовать для быстрого и простого вычисления среднего значения.
| Средняя гармоническая невзвешенная (СГН) | Средняя арифметическая невзвешенная (САН) |
|---|---|
| Учитывает инверсии и пропорции | Не учитывает инверсии и пропорции |
| Устойчива к выбросам и неравномерным значениям | Простой и быстрый метод вычисления |
| Подходит для измерений скорости или силы | Часто используется в экономике и статистике |
Видео:Средние величины. Средняя гармоническая.Скачать

Преимущества использования средней гармонической невзвешенной
1. Учет всех значений в выборке: Средняя гармоническая невзвешенная учитывает все значения в выборке, в отличие от средней арифметической, которая может быть смещена в сторону больших или маленьких значений.
2. Взвешивание низких значений: Средняя гармоническая невзвешенная уделяет больше внимания низким значениям, что делает ее полезной в случаях, когда низкие значения имеют большую значимость. Например, при расчете средней скорости, средняя гармоническая невзвешенная поможет учесть время, затраченное на преодоление препятствий, таких как перепады высоты или противоштормовое движение.
3. Применимость в финансовых расчетах: Средняя гармоническая невзвешенная часто используется в финансовых расчетах, таких как расчет доходности инвестиций или оценка рисков. Это связано с тем, что она учитывает абсолютные изменения величин и позволяет более точно оценить темп роста или падения.
4. Устойчивость к выбросам: Средняя гармоническая невзвешенная более устойчива к выбросам, по сравнению с средней арифметической. Она менее подвержена влиянию крайних значений и позволяет получить более устойчивую оценку среднего.
5. Использование в экологических и биологических исследованиях: Средняя гармоническая невзвешенная широко применяется в экологических и биологических исследованиях, где важно учесть пропорциональное влияние различных факторов на общую характеристику. Это может быть полезно, например, при расчете средней глубины океана или средней нагрузки на популяцию животных.
6. Математическая устойчивость: Средняя гармоническая невзвешенная обладает некоторыми математическими свойствами, которые делают ее удобной для использования в анализе данных. Например, она можно выразить в виде взвешенной суммы относительных значений, что позволяет легче проводить арифметические операции.
Более точный показатель среднего значения
Средняя гармоническая невзвешенная альтернатива средней арифметической невзвешенной представляет собой более точный показатель среднего значения. Она используется для учета различий в весе или значимости значений, что делает ее особенно полезной при работе с наборами данных, где некоторые значения имеют большее влияние, чем другие.
В отличие от средней арифметической, которая просто суммирует все значения и делит их на количество значений, средняя гармоническая учитывает обратное значение каждого значения. Это дает больший вес более низким значениям и меньший вес высоким значениям. В результате, средняя гармоническая более чувствительна к низким значениям и имеет меньшую подверженность выбросам.
Применение средней гармонической невзвешенной альтернативы средней арифметической невзвешенной может быть полезно во многих областях. Например, она может быть использована для расчета среднего значения финансовых показателей, таких как доходность инвестиций или прибыльность компании. В таких случаях, когда некоторые значения имеют большое влияние на общий результат, средняя гармоническая может дать более точную оценку среднего значения.
📺 Видео
Среднее арифметическое. Размах. Мода. Медиана. Алгебра, 7 классСкачать

Статистика. Средние величиныСкачать

Средние величины. Средняя арифметическая.Скачать
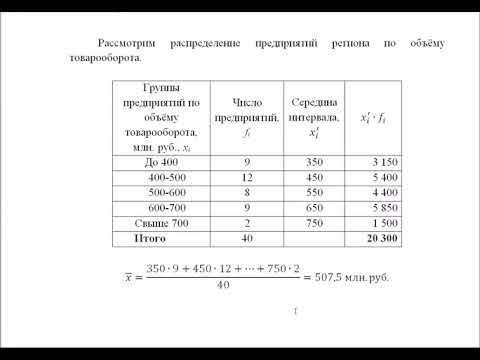
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ #shorts #математика #егэ #огэ #профильныйегэСкачать

Среднее арифметическое и медиана - отличия и свойства.Скачать

Арифметическая и геометрическая прогрессия | Математика TutorOnlineСкачать

Арифметическая прогрессия 9 класс. Формулы, о которых вы не знали | МатематикаСкачать

Среднее гармоническое трёх чисел a, b и c вычисляется по формуле h = ((1/a + 1/b + 1/c) / 3))^-1.Скачать

Мода, размах, среднее арифметическое, медианаСкачать

Алгебра 8 класс (Урок№50 - Дисперсия и среднее квадратичное отклонение.)Скачать

Среднее гармоническое. Средняя скорость. Причём тут планиметрия?Скачать
Домашнее задание. C++. Сумма, произведение, среднее арифметическое чисел.Скачать

Арифметическая и геометрическая прогрессия в ОГЭ | Математика ОГЭ 2022 | УмскулСкачать

Элементы статистики. Дисперсия. Стандартное отклонениеСкачать

Арифметическая прогрессия. Формула n-го члена арифметической прогрессии. 9 класс.Скачать
Среднее арифметическое и среднее геометрическоеСкачать
