Как вычислить гипотенузу, если известен один катет и угол, равный 30 градусам

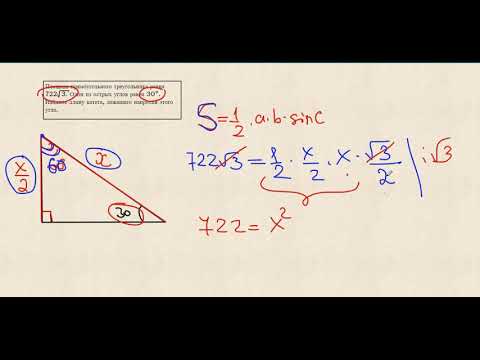
В математике существует прекрасная формула для расчета гипотенузы прямоугольного треугольника, если известен только один катет и угол между гипотенузой и этим катетом. Если вам дан прямоугольный треугольник, угол в котором равен 30 градусам, а один из катетов известен, вы можете применить эту формулу и легко найти гипотенузу.

Для начала, обратите внимание на то, что угол в 30 градусов соответствует одному из особых треугольников, называемому равносторонним. В равностороннем треугольнике все стороны и углы равны между собой. Если у вас есть равносторонний треугольник, справедливо, что все его углы равны 60 градусам.

Зная данное правило, вы можете рассматривать угол в 30 градусов как половину угла в равностороннем треугольнике и использовать его для расчета гипотенузы. Формула для этого расчета такова: гипотенуза равна удвоенному катету, умноженному на тангенс половины угла.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Как определить гипотенузу по катету и углу в 30 градусов?

Для начала, вспомним, что гипотенуза — это наибольшая сторона прямоугольного треугольника, лежащая против прямого угла. Катеты же — это две меньшие стороны треугольника, которые формируют прямой угол.

Чтобы определить гипотенузу по катету и углу в 30 градусов, воспользуемся тригонометрическим соотношением для синуса угла:

sin(угол) = противолежащий катет / гипотенуза

Так как нам известен угол в 30 градусов, мы можем записать следующую формулу:

sin(30 градусов) = катет / гипотенуза

Теперь осталось лишь решить эту формулу относительно гипотенузы:

гипотенуза = катет / sin(30 градусов)

Обратите внимание, что тут мы используем sin(30 градусов), потому что sin(30 градусов) равен 0.5, что является известным значением.

Итак, чтобы найти гипотенузу по катету и углу в 30 градусов, нужно разделить значение катета на sin(30 градусов) (то есть 0.5):

гипотенуза = катет / 0.5

Таким образом, чтобы определить гипотенузу по катету и углу в 30 градусов, нужно разделить значение катета на 0.5.

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Что такое гипотенуза и катет?

Катеты — это две меньшие стороны треугольника и примыкающие к прямому углу. Они образуют его основание и ортогонально пересекаются в этой точке. Катеты являются определяющими характеристиками прямоугольного треугольника и участвуют в вычислении гипотенузы и других параметров.

Определение гипотенузы

Если известен катет (сайн), противолежащий углу 30 градусов, и угол (гипотенуза) в 30 градусов, можно воспользоваться формулой:

Гипотенуза = катет / sin(угол)

Подставив известные значения, можно вычислить длину гипотенузы и определить размеры прямоугольного треугольника.

Определение катета

Если известны гипотенуза и угол в 30 градусов, то катет можно найти с помощью тригонометрических функций. В данном случае, известная гипотенуза является противолежащей стороной угла в 30 градусов, а катет – прилежащая сторона. Для нахождения катета можно использовать функцию синуса угла 30 градусов:

sin(30°) = катет / гипотенуза

Для выражения катета через гипотенузу и синус угла, можно переставить члены уравнения:

катет = гипотенуза * sin(30°)

Таким образом, зная значение гипотенузы и угла в 30 градусов, можно определить значение катета с помощью тригонометрической функции синуса.

Видео:7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Как найти гипотенузу по катету и углу в 30 градусов?

Для решения данной задачи необходимо знать значение синуса или косинуса угла 30 градусов. Так как в данной задаче угол измеряется в 30 градусов, нам понадобится значение синуса этого угла.

Зная значение синуса угла 30 градусов, длину катета можно умножить на значение синуса угла, чтобы получить значение гипотенузы. Формула будет выглядеть следующим образом:

Гипотенуза = Катет * Синус(30 градусов)

Решая эту формулу, можно найти значение гипотенузы. Для точного результата важно убедиться в том, что используется правильное значение синуса угла 30 градусов.

Теперь, зная как найти гипотенузу по катету и углу в 30 градусов, вы можете применить этот метод для решения задач, связанных с прямоугольными треугольниками, где известны катет и угол в 30 градусов.

Использование библиотеки математических функций

Для начала нужно найти длину противолежащего катета. Известно, что в прямоугольном треугольнике с углом в 30 градусов длина гипотенузы равна двум катетам. Поэтому, если известна длина одного катета, то длина другого катета будет равна половине длины гипотенузы.

Пусть x — длина известного катета. Тогда длина противолежащего катета будет равна x / 2.

Далее, используя функцию Math.sin(), можно найти синус угла в 30 градусов. Синус 30 градусов равен 0.5, поэтому можно записать уравнение:

0.5 = (x / 2) / гипотенуза

Домножим обе части уравнения на гипотенузу:

гипотенуза * 0.5 = x / 2

Умножим обе части уравнения на 2 для того, чтобы избавиться от деления на 2:

гипотенуза = x

Таким образом, длина гипотенузы равна длине известного катета.

Теперь, зная длину гипотенузы и одного катета, можно найти длину противолежащего катета, используя теорему Пифагора:

длина противолежащего катета = √(гипотенуза^2 — катет^2)

Подставим известные значения:

длина противолежащего катета = √(гипотенуза^2 — x^2)

Следовательно, для решения задачи можно использовать эти математические формулы и функции из библиотеки математических функций.

Применение тригонометрических функций

Одно из основных применений тригонометрических функций — нахождение недостающих параметров треугольников. Например, для определения гипотенузы треугольника, если известен катет и угол, можно воспользоваться тригонометрической функцией синуса.

Синус угла в треугольнике определяется как отношение противолежащей стороны к гипотенузе. Для нахождения гипотенузы треугольника по известному катету и углу в 30 градусов, можно воспользоваться формулой:

гипотенуза = катет / sin(угол)

В данном случае, где катет известен и равен X, а угол равен 30 градусов, формула примет вид:

гипотенуза = X / sin(30°)

Подставив численное значение синуса 30 градусов (0.5), получим окончательную формулу:

гипотенуза = 2X.

Таким образом, для нахождения гипотенузы треугольника, если известен катет и угол в 30 градусов, следует умножить значение катета на 2.

Видео:Теорема Пифагора для чайников)))Скачать

Рассчет гипотенузы в практическом примере

Для рассчета гипотенузы прямоугольного треугольника, нужно знать значение одного из катетов и угол между ними. Рассмотрим практический пример на рисунке.

Допустим, у нас есть прямоугольный треугольник ABC, где AB — катет, BC — гипотенуза и угол B равен 30 градусов.

Согласно теореме синусов, отношение длин противолежащей стороны к гипотенузе равно синусу угла: sin(B) = AB/BC.

Таким образом, гипотенуза BC равна катету AB, деленному на синус угла B: BC = AB / sin(B).

Подставляя известные значения, получаем: BC = AB / sin(30).

Пользуясь таблицей значений синуса, находим sin(30) = 0.5. Подставляя, получаем: BC = AB / 0.5.

Итак, для нахождения гипотенузы в данном примере, необходимо значение катета AB разделить на 0.5, то есть BC = 2 * AB.

Определение значения катета

Формула для определения значения катета:

катет = гипотенуза * sin(угол)

Угол указывается в градусах. Функция синуса возвращает отношение противолежащего катета к гипотенузе. Подставив известные значения в формулу, можно получить значение катета.

Например, если известен угол в 30 градусов и гипотенуза равна 10 см, можно определить значение катета следующим образом:

катет = 10 * sin(30)

катет ≈ 5 см

Таким образом, зная гипотенузу и угол в прямоугольном треугольнике, можно легко определить значение катета, используя функцию синуса.

Вычисление гипотенузы по формуле

Для вычисления длины гипотенузы треугольника, если известны катет и угол в 30 градусов, можно использовать следующую формулу:

гипотенуза = катет / sin(угол)

где:

• гипотенуза — длина гипотенузы треугольника;
• катет — длина известного катета треугольника;
• угол — величина известного угла в градусах.

Для нахождения синуса угла в 30 градусов можно воспользоваться таблицей значений или калькулятором:

sin(30°) ≈ 0.5

Теперь можем подставить известные значения в формулу:

гипотенуза = катет / 0.5

Таким образом, длина гипотенузы будет равна половине длины известного катета, то есть гипотенуза в два раза длиннее катета.

Если известна длина катета, но требуется найти длину гипотенузы, можно использовать эту формулу для вычисления.

📺 Видео

Катет напротив 30° равен половине гипотенузыСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Катеты и гипотенузаСкачать

Урок 1. Почему катет, лежащий напротив 30 градусов равен половине гипотенузы? №15 ОГЭ.Скачать

№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

Урок 22. Свойство катета прямоугольного треугольника, лежащего против угла в 30° (7 класс)Скачать

ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА 30, 45 И 60 ГРАДУСОВСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Определение длины гипотенузыСкачать

8 класс, 30 урок, Значения синуса, косинуса и тангенса для углов 30◦, 45◦ и 60◦Скачать

Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

ОГЭ 16 задание. Найти гипотенузу, если известен катет и синусСкачать

Лайфхак нахождения катета в прямоугольном треугольникеСкачать

По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Известна площадь прямоугольного треугольника и один из острых углов. Найти противолежащий катетСкачать

Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать