Призма — это геометрическое тело, которое обладает двумя равными и параллельными основаниями, соединенными боковыми гранями. Различные параметры призмы, такие как ее высота, основания и боковые ребра, позволяют вычислить различные характеристики этого тела, включая ее объем и полную поверхность.
Полная поверхность призмы — это сумма площадей всех ее граней. Чтобы вычислить полную поверхность призмы, необходимо знать площади оснований и площади боковых граней. Также важно понимать, что если основания призмы являются правильными многоугольниками, то боковые грани призмы будут прямоугольниками.
Для расчета полной поверхности призмы нужно умножить площадь основания на число граней, а затем добавить площади боковых граней. Пользуясь формулами для нахождения площадей различных фигур, можно выразить полную поверхность призмы через известные параметры, такие как высота призмы, длины ребер и углы оснований.
- Зачем нужно знать состав полной поверхности призмы?
- Понимание особенностей призмы помогает в…
- 1. Решение геометрических задач
- 2. Изучение оптики
- 3. Проектирование и архитектура
- 4. Наука и исследования
- 5. Технические применения
- Важная информация при использовании призмы:
- Уровень прозрачности:
- Отражение и преломление:
- Методы определения полной поверхности призмы:
- Использование алгоритма:
- Использование геометрических формул:
- 💡 Видео
Видео:Геометрия 10 класс (Урок№14 - Призма.)Скачать

Зачем нужно знать состав полной поверхности призмы?
Основные составляющие полной поверхности призмы включают в себя:
| Элемент | Описание |
|---|---|
| Грани | Призма имеет две параллельные грани, которые называют основаниями, и боковые грани, соединяющие основания. Грани являются плоскими поверхностями, которые задают форму и размеры призмы. |
| Ребра | Ребра призмы соединяют соответствующие вершины оснований. Ребра определяют длину и форму призмы и служат основой для расчета объема и площади поверхности. |
| Вершины | Вершины призмы являются точками пересечения ребер. Вершины помогают определить форму и размеры призмы и служат в качестве ориентировки при изучении ее свойств и характеристик. |
Знание состава полной поверхности призмы помогает углубить наши знания об этой геометрической фигуре и применить их на практике. Например, понимание всех составляющих призмы пригодится при вычислении ее объема или площади поверхности. Знание состава призмы также помогает нам решать задачи по геометрии и применять полученные знания в реальных ситуациях.
Видео:Площадь поверхности призмы. 11 класс.Скачать

Понимание особенностей призмы помогает в…
1. Решение геометрических задач
Призма представляет собой трехмерную фигуру с двумя равными и параллельными базами, которые соединены боковыми гранями. Различные геометрические задачи, связанные с призмами, могут требовать рассчета объема, площади поверхности или длины диагонали. Знание формул и свойств призмы позволяет решать эти задачи более эффективно и точно.
2. Изучение оптики
Призмы имеют важное значение в области оптики. Они способны изменять направление падающего света и отделять свет на разные спектры. Призмы используются в различных оптических приборах, таких как бинокли, телескопы, микроскопы и спектральные анализаторы. Правильное понимание принципов работы призмы помогает в разработке и улучшении оптических систем.
3. Проектирование и архитектура
Призмы используются в архитектурном дизайне для создания уникальных эффектов и игры света. Использование призм может изменять восприятие пространства, добавлять интересные рефлексы и отражения. Понимание, как свет взаимодействует с призмами, позволяет архитекторам и дизайнерам создавать уникальные и впечатляющие структуры.
4. Наука и исследования
Призмы широко применяются в научных исследованиях во многих областях, включая физику, химию, биологию и геологию. Они используются для анализа химических составов, изучения свойств материалов, исследования структуры кристаллов и многое другое. Знание о призмах и их свойствах является важным для проведения точных и надежных экспериментов и исследований.
5. Технические применения
Призмы имеют широкое применение в различных технических областях. Они используются в лазерных системах для направления и фокусировки лазерного луча, в камерах для коррекции и сегментации изображений, в оптических светофильтрах и датчиках, а также в многочисленных других устройствах. Понимание особенностей призмы позволяет разрабатывать и улучшать такие технические системы.
В итоге, глубокое понимание особенностей призмы не только расширяет наши знания в физике и геометрии, но и способствует решению практических задач в различных областях науки и техники.
Видео:10 класс, 30 урок, ПризмаСкачать

Важная информация при использовании призмы:
1. Правильная установка:
Перед использованием призмы важно правильно установить ее на плоскую поверхность. Ориентируйтесь на грани призмы, чтобы оптимально выставить ее углы. Также обратите внимание на освещение, чтобы избежать возникновения ненужных бликов.
2. Особые применения:
Призмы имеют множество применений в разных областях. Например, они используются в оптике для изменения направления светового луча и получения спектра. В геометрии призмы используются для измерения объемов тел и определения площади их поверхности. Также призмы находят применение в фотографии и видеозаписи для создания особых эффектов и перспектив.
3. Понимание поверхности призмы:
Полная поверхность призмы состоит из двух оснований и боковых граней. Основания представляют собой прямоугольники или многоугольники, а боковые грани соединяют основания и образуют боковую поверхность призмы. Для вычисления полной поверхности призмы необходимо сложить площади всех граней.
4. Составление формулы:
Чтобы вычислить полную поверхность призмы, нужно использовать формулу: S = 2Sосн + Sбок, где S — полная поверхность призмы, Sосн — площадь основания призмы, Sбок — площадь боковой поверхности призмы. Учтите, что для каждого типа призмы формула может отличаться.
5. Проверка результатов:
После вычисления полной поверхности призмы всегда стоит проверять результат. Проверьте правильность использования формулы и точность вычислений. При необходимости проведите дополнительные измерения и проверки, чтобы исключить возможные ошибки.
Пользуйтесь этой информацией для успешного использования призмы и достижения нужных результатов!
Уровень прозрачности:
Уровень прозрачности входит в состав полной поверхности призмы и играет ключевую роль в определении ее внешнего вида и функциональности. Прозрачность определяется способностью призмы пропускать свет через себя.
Уровень прозрачности может быть различным и зависит от материала, из которого изготавливается призма. Некоторые призмы изготовляются из полностью прозрачных материалов, таких как стекло или оптический кристалл, и имеют высокую пропускную способность для света.
Другие призмы могут быть изготовлены из полупрозрачных материалов, таких как пластик или полимеры, и иметь более низкую пропускную способность для света.
Уровень прозрачности призмы может быть также регулируемым путем нанесения специальных покрытий или использования фильтров. Это позволяет контролировать количество света, проходящего через призму, и создавать различные эффекты и оттенки.
Важно отметить, что прозрачность призмы может также зависеть от условий освещения и угла наблюдения. При изменении этих параметров уровень прозрачности может быть воспринят по-разному.
Отражение и преломление:
Отражение света — это процесс, при котором свет отражается от поверхности призмы. Отражение происходит под углом, равным углу падения. Это явление объясняется законом отражения света, согласно которому угол падения равен углу отражения.
Преломление света — это процесс, при котором свет проникает через поверхность призмы и меняет свое направление. Величина изменения направления света зависит от оптических свойств материала призмы и от угла падения света на поверхность призмы. Оптические свойства материала призмы определяются его показателем преломления.
Отражение и преломление являются фундаментальными явлениями в оптике и широко используются в различных оптических приборах, таких как линзы, зеркала, призмы и т.д. Знание этих явлений позволяет понять, как работают и какие эффекты создают данные оптические приборы.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Методы определения полной поверхности призмы:
Существуют несколько методов определения полной поверхности призмы:
- Метод разбиения на грани. При данном методе необходимо разделить всю поверхность призмы на отдельные грани и вычислить площадь каждой грани отдельно. Затем полученные площади нужно сложить, чтобы получить полную поверхность.
- Метод оснований и боковой поверхности. Суть данного метода заключается в вычислении площадей оснований и боковой поверхности призмы. Площади оснований равны площадям соответствующих фигур (круга, треугольника и т.д.), а площадь боковой поверхности можно найти, зная периметры оснований и высоту призмы.
- Метод разностных площадей. Этот метод основан на простой формуле: полная поверхность призмы равна сумме площади поверхности аналогичного параллелепипеда и площади срезанных углов. Причем площадь срезанных углов находится как разница между полной поверхностью параллелепипеда и площадями оснований.
Выбор метода зависит от особенностей призмы и доступных данных для вычислений.
Использование алгоритма:
Для того чтобы рассчитать полную поверхность призмы, следует выполнить несколько шагов:
- Подсчитайте площади всех граней призмы. Для прямоугольной призмы, это можно сделать, умножив длину на ширину каждой грани.
- Просуммируйте все полученные значения площадей граней.
- Итоговая сумма является полной поверхностью призмы.
Для лучшего понимания процесса, можно воспользоваться таблицей, где каждая строка представляет собой отдельную грань призмы. В столбцах указываются размеры каждой грани, а также полученная площадь:
| Грань | Длина | Ширина | Площадь |
|---|---|---|---|
| Грань 1 | а | b | a * b |
| Грань 2 | а | c | a * c |
| Грань 3 | b | c | b * c |
| Грань 4 | а | b | a * b |
| Грань 5 | а | c | a * c |
| Грань 6 | b | c | b * c |
Проводя вычисления с использованием данной таблицы, можно получить сумму всех площадей граней и, таким образом, определить полную поверхность призмы.
Использование геометрических формул:
Для определения полной поверхности призмы необходимо использовать геометрические формулы. Полная поверхность призмы состоит из площадей ее боковой поверхности и оснований.
Формула для нахождения площади боковой поверхности призмы:
Sб = p × h,
где p — периметр основания призмы, а h — высота призмы.
Формула для нахождения площади основания призмы зависит от ее формы:
— Для прямоугольной призмы:
Sосн = a × b,
где a и b — длины сторон прямоугольника, являющегося основанием призмы.
— Для треугольной призмы:
Sосн = ½ × a × h,
где a — длина основания треугольника, а h — высота треугольника.
Для определения полной поверхности призмы нужно сложить площади боковой поверхности и оснований:
Sполн = 2Sб + Sосн.
Подставляя соответствующие значения в формулы, можно вычислить полную поверхность призмы.
💡 Видео
Площадь полной поверхности призмыСкачать

Задания 11, 13 (часть 2) | ЕГЭ 2024 Математика (база) | ПризмаСкачать

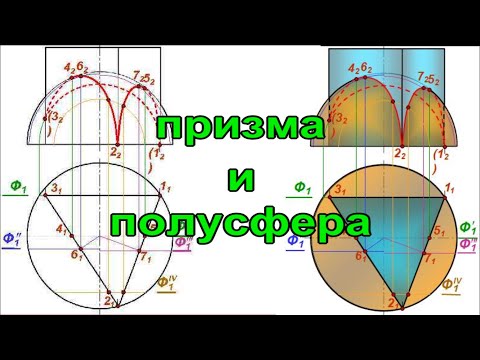
Пересечение поверхностей призмы и полусферы. Пошаговое видео. Инженерная графикаСкачать
Видеоурок по математике "Цилиндр"Скачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

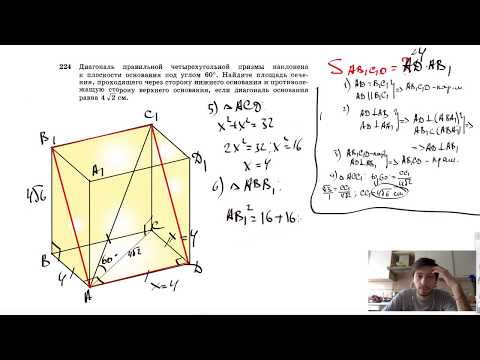
№224. Диагональ правильной четырехугольной призмы наклонена к плоскости основания под углом 60°Скачать
Геометрия 10 кл ПризмаСкачать

Правильная треугольная призмаСкачать

Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Арифметическая прогрессия 9 класс. Формулы, о которых вы не знали | МатематикаСкачать

ЕГЭ. Математика. Площади поверхности и объемы геометрических тел. ПрактикаСкачать

РАЗБОР ВСЕХ ПРОТОТИПОВ ЗАДАНИЯ 3 ПРОФИЛЬНОГО ЕГЭ МАТЕМАТИКА 2024 | ПРИЗМЫСкачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать
