Как найти среднее число в множестве найти середину с помощью функции (3 видео)

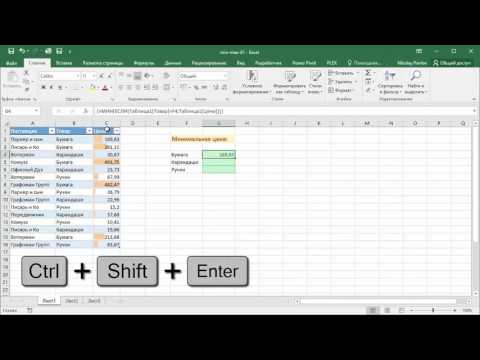
Определение среднего числа в множестве является одной из наиболее распространенных задач при работе с числами. Чтобы найти среднее число, нужно просуммировать все числа в множестве и разделить полученную сумму на количество чисел.

Однако, помимо нахождения среднего числа, иногда требуется найти середину множества, то есть значение, которое расположено между наименьшим и наибольшим числами. Для этого можно воспользоваться функцией, которая сортирует числа по возрастанию и возвращает число, находящееся по середине. Если количество чисел четное, то выбирается значение, находящееся слева от центра.

Примером такой функции может быть функция median, которая принимает массив чисел в качестве параметра и возвращает среднее значение. Если количество чисел в массиве четное, функция выбирает два значения посередине и делит их на два, чтобы получить среднее значение.

Содержание

Определение Среднего числа
Понятие среднего числа
Значение среднего числа в математике
Как выбрать среднее число
Среднее арифметическое
Как найти среднее арифметическое
Примеры использования среднего арифметического
Медиана и среднее значение
Чем отличается медиана от среднего значения
Как найти медиану
Функция для нахождения среднего числа
Описание функции
Примеры использования функции
🎥 Видео

Видео:Как посчитать среднее значение в Excel (среднее арифметическое в Экселе) — Функция СРЗНАЧ (AVERAGE)Скачать

Определение Среднего числа

Если множество содержит четное количество чисел, то среднего числа не существует, так как два числа расположены ровно посередине. В этом случае можно найти среднее арифметическое двух чисел, которые находятся посередине. Для этого их нужно сложить и разделить на 2.

Среднее число имеет важное значение в различных областях, например, в статистике. Оно может быть использовано для оценки центральной тенденции набора данных и является одним из способов представления среднего значения.

Определение среднего числа помогает нам понять центральное значение в множестве чисел и использовать это значение в дальнейших вычислениях или анализе данных.

Видео:Как посчитать среднее значение в ExcelСкачать

Понятие среднего числа

Среднее число определяется путем суммирования всех чисел выборки и деления этой суммы на количество чисел. Таким образом, среднее число является статистической мерой центральной тенденции.

Для большинства случаев, среднее число является хорошей мерой для представления «типичного» значения в выборке, так как оно учитывает все числа и сглаживает экстремальные значения.

Среднее число может быть рассчитано для различных типов чисел, включая целые, дробные, положительные, отрицательные и непрерывные числа.

Значение среднего числа в математике

Чтобы найти среднее число в множестве, необходимо сложить все числа в наборе и разделить полученную сумму на количество чисел. Например, если у нас есть набор чисел {2, 4, 6, 8, 10}, то среднее число будет равно (2 + 4 + 6 + 8 + 10) / 5 = 6.

Однако следует помнить, что среднее число может быть искажено выбросами или несбалансированным распределением чисел в наборе. В таких случаях рекомендуется использовать другие меры центральной тенденции, такие как медиана или мода, чтобы получить более репрезентативное представление о данных.

В математике существуют различные методы для нахождения среднего числа, включая арифметическое среднее, взвешенное среднее и гармоническое среднее. Каждый из этих методов имеет свои особенности и может быть использован в зависимости от конкретной задачи.

Как выбрать среднее число

Для нахождения среднего числа в множестве можно использовать функцию. Ниже приведен пример функции на языке программирования Python, которая рассчитывает среднее число:

Python код

Python код
`def calculate_average(numbers): sum = 0 count = 0 for number in numbers: sum += number count += 1 average = sum / count return average numbers = [1, 2, 3, 4, 5] average = calculate_average(numbers) print("Среднее число:", average)`


def calculate_average(numbers):
sum = 0
count = 0
for number in numbers:
sum += number
count += 1
average = sum / count
return average
numbers = [1, 2, 3, 4, 5]
average = calculate_average(numbers)
print("Среднее число:", average)

В данной функции переменная numbers представляет собой множество чисел, для которого необходимо найти среднее число. Функция проходит по каждому числу в множестве, суммирует их и подсчитывает их количество. Затем, делит сумму на количество и возвращает полученное значение.

Таким образом, вы можете использовать данную функцию для нахождения среднего числа в любом множестве чисел, подобных приведенному в примере.

Видео:4 Функция СРЗНАЧЕСЛИ и расчет средней арифметической взвешенной в ExcelСкачать

Среднее арифметическое

Для нахождения среднего арифметического чисел следует выполнить следующий алгоритм:

Пройти по всем числам в множестве.
Сложить все числа вместе.
Разделить полученную сумму на количество чисел в множестве.

Пример:

Множество чисел	Сумма чисел	Количество чисел	Среднее арифметическое
4, 6, 8, 10	28	4	7
3, 7, 9, 12	31	4	7.75

Среднее арифметическое может быть полезно в различных сферах, например, в статистике, экономике, физике, и т.д. Оно позволяет получить общую характеристику набора чисел, а также упрощает их сравнение и анализ.

Как найти среднее арифметическое

Чтобы найти среднее арифметическое, необходимо выполнить следующие шаги:

Сложите все числа в множестве. Например, если у нас есть множество чисел {2, 4, 6, 8}, то сумма будет равна 20.
Посчитайте количество чисел в множестве. В данном примере у нас 4 числа.
Разделите сумму на количество чисел. В нашем примере это будет равно 20 / 4 = 5.

Таким образом, среднее арифметическое данного множества чисел равно 5.

Среднее арифметическое является важным показателем, который помогает оценить общую характеристику числового ряда. Оно также может быть использовано для сравнения различных множеств и выявления отклонений от среднего значения.

Использование среднего арифметического позволяет нам упростить и описать данные с помощью одного числа, что существенно облегчает их анализ и понимание.

Примеры использования среднего арифметического

Пример	Описание
Оценки учеников	В учебном заведении считается итоговая оценка каждого ученика путем нахождения среднего арифметического его оценок по предметам. Это позволяет определить общую успеваемость ученика и сравнивать его с другими.
Статистика продаж	В бизнесе среднее арифметическое используется для анализа статистики продаж. Например, можно вычислить средний чек клиентов или среднее количество продаж в определенный период времени. Это поможет определить эффективность бизнеса и выявить тенденции.
Медицина	В медицине среднее арифметическое используется для оценки показателей здоровья пациентов. Например, можно вычислить средний уровень артериального давления или средний возраст заболевших. Это помогает определить нормальные значения и выявить аномалии.
Инженерия	В инженерии среднее арифметическое используется для анализа различных параметров и измерений. Например, можно вычислить среднюю скорость движения объекта или средний уровень шума в определенной зоне. Это помогает определить эффективность системы и принять соответствующие меры.

Приведенные примеры демонстрируют широкий спектр применения среднего арифметического и его значимость в решении различных задач. Важно уметь правильно использовать эту концепцию и проводить соответствующие анализы.

Видео:Как найти среднее значение в экселеСкачать

Медиана и среднее значение

Среднее значение, также известное как среднее арифметическое, находится путем деления суммы всех чисел на количество чисел в наборе. Например, если у нас есть набор чисел 1, 2, 3, 4, 5, среднее значение будет равно (1 + 2 + 3 + 4 + 5) / 5 = 3.

Среднее значение чувствительно к выбросам в данных, поскольку оно учитывает все числа в наборе. Это означает, что даже одно крайнее значение может значительно искажать среднее значение. Поэтому при использовании среднего значения важно быть внимательным к выбросам.

Медиана, с другой стороны, является значением, которое находится в середине упорядоченного набора чисел. Для нашего примера с набором чисел 1, 2, 3, 4, 5, медиана будет равна 3. Если у нас есть четное количество чисел, медиана находится путем нахождения среднего значения двух средних чисел.

Медиана является более устойчивой мерой центральной тенденции и менее подвержена влиянию выбросов. Она удобна для использования в случаях, когда есть одно или несколько выбросов в данных.

Таким образом, использование среднего значения или медианы зависит от характера данных и вопросов, которые мы пытаемся решить. Оба показателя имеют свои преимущества и ограничения, и мы должны выбирать их с учетом контекста и целей исследования.

Пример набора чисел	Среднее значение	Медиана
1, 2, 3, 4, 5	3	3
1, 2, 3, 4, 100	22	3
1, 2, 3, 4, 1000	202	3

Чем отличается медиана от среднего значения

При анализе данных, находящихся в наборе, может возникнуть необходимость определить центральное значение. В этом случае можно использовать медиану или среднее значение. Однако, эти две меры центральной тенденции имеют разные подходы к определению «типичного» значения в наборе данных.

Среднее значение, или среднее арифметическое, основывается на сумме всех значений в наборе данных, деленной на их количество. Это дает общую идею о средней величине в наборе данных и подходит для равномерно распределенных данных.

Медиана, с другой стороны, находится в середине упорядоченного набора данных. Если число элементов в наборе данных нечетное, медиана представляет собой значение, которое находится точно в середине. Если число элементов четное, медиана является средним значением двух центральных элементов. Медиана часто используется в случаях, когда в данных присутствуют выбросы или асимметричное распределение.

Таким образом, различия между медианой и средним значением заключаются в том, что среднее значение учитывает все значения в наборе данных, в то время как медиана фокусируется только на середине упорядоченных данных.

Как найти медиану

Для нахождения медианы, необходимо выполнить следующие шаги:

Упорядочить множество чисел по возрастанию.
Если количество чисел в множестве нечетное, то медиана находится в середине списка.
Если количество чисел в множестве четное, то медиана находится между двумя центральными числами. Для этого необходимо найти среднее значение этих двух чисел.

Например, рассмотрим множество чисел: 5, 8, 2, 9, 4.

Сначала упорядочим его по возрастанию: 2, 4, 5, 8, 9.

Так как количество чисел в множестве нечетное, медиана будет равна 5.

Если в множестве было бы четное количество чисел, например: 2, 4, 5, 8, 9, 12.

После упорядочивания получим следующий список: 2, 4, 5, 8, 9, 12.

Так как количество чисел в множестве четное, медиана будет равна среднему значению центральных чисел: (5 + 8) / 2 = 6.5.

Итак, для нахождения медианы нужно упорядочить множество чисел и выбрать среднее число или среднее значение двух центральных чисел, в зависимости от количества чисел в множестве.

Количество чисел в множестве	Медиана
Нечетное	Среднее число в середине списка
Четное	Среднее значение двух центральных чисел

Видео:Как в экселе посчитать среднее значениеСкачать

Функция для нахождения среднего числа

Для нахождения среднего числа в множестве можно использовать специальную функцию, которая суммирует все числа и делит их на их количество.

В следующей таблице приведен пример функции на языке программирования Python, которая находит среднее число в заданном списке:

Номер строки	Код	Описание
1	`def find_average(numbers):`	Объявление функции с одним аргументом — списком чисел
2	`total = sum(numbers)`	Суммируем все числа из списка
3	`average = total / len(numbers)`	Делим сумму на количество чисел в списке
4	`return average`	Возвращаем полученное среднее число

В данной функции используется встроенная функция «sum», которая суммирует все элементы списка, а также функция «len», которая возвращает количество элементов в списке.

Приведенный пример демонстрирует, как можно определить среднее число в списке, однако функцию можно изменить в соответствии с требованиями и особенностями каждой конкретной задачи.

Описание функции

Для нахождения среднего числа в множестве и поиска середины с помощью функции предлагается использовать следующий алгоритм:

1. Создайте функцию с именем «findAverage», которая будет принимать один параметр — множество чисел.

2. Внутри функции объявите переменную «sum» и присвойте ей значение 0.

3. Используя цикл «for of», пройдитесь по каждому числу в множестве. На каждой итерации прибавьте текущее число к переменной «sum».

4. После завершения цикла, найдите длину множества с помощью свойства «size» и присвойте ее переменной «length».

5. Вычислите среднее число, разделив сумму всех чисел на их количество: «average = sum / length».

6. Верните найденное среднее число из функции, используя оператор «return».

Пример использования функции:


let numbers = [1, 2, 3, 4, 5];
let average = findAverage(numbers);

В приведенном примере функция «findAverage» принимает массив чисел и возвращает их среднее число, которое равно 3.

Примеры использования функции

Функция для нахождения среднего числа в множестве может быть полезной во многих ситуациях. Вот несколько примеров, как ее можно использовать:

Расчет среднего возраста группы людей. Если вам нужно найти средний возраст людей в определенной группе, вы можете использовать функцию для нахождения среднего числа, чтобы получить точный результат.
Определение среднего времени выполнения задачи. Если у вас есть несколько задач, которые занимают разное время, функция для нахождения среднего числа поможет вам определить среднее время выполнения этих задач.
Вычисление среднего значения оценок студентов. Если вы имеете оценки студентов по разным предметам, функция для нахождения среднего числа поможет вам узнать среднюю оценку по каждому предмету.

Все эти примеры показывают, насколько полезной может быть функция для нахождения среднего числа в множестве. Она помогает получить точные и релевантные данные, которые могут быть использованы для принятия важных решений.