Порядок операций в арифметике плюс или минус впереди (2 видео)

Арифметика – это базовая область математики, которая изучает числа, их свойства и операции над ними. Основными операциями в арифметике являются сложение, вычитание, умножение и деление. Порядок выполнения этих операций имеет важное значение для получения правильного результата.

Один из вопросов, которые часто возникают при работе с арифметикой, связан с порядком операций, когда перед числом стоит знак плюс или минус. Нужно ли сначала выполнить операцию сложения или вычитания, а затем производить умножение и деление? Ответ на этот вопрос зависит от правил, которые были установлены в математике.

Правила порядка операций позволяют определить, в какой последовательности следует выполнять операции в выражениях. Обычно в арифметике применяется правило, согласно которому сначала выполняются операции умножения и деления, а затем сложения и вычитания. Однако, когда перед числом стоит знак плюс или минус, порядок операций может изменяться, что может привести к разным результатам. Важно понимать, как правильно применять эти правила в конкретных ситуациях, чтобы избежать ошибок и получить верный ответ.

Содержание

Существующие правила
Правило умножения и деления
Правило сложения и вычитания
Знаки операций и их применение
Знаки операций впереди числа: плюс
Знаки операций впереди числа: минус
Влияние знака операции на результат
Сложение и вычитание с разными знаками
Умножение и деление с разными знаками
Порядок операций и приоритеты
Использование скобок
Порядок операций в комплексных выражениях
Особые случаи и исключения
Применение отрицательных чисел
📸 Видео

Видео:Порядок выполнения действий в выражениях. Числовые выраженияСкачать

Существующие правила

В арифметике существуют определенные правила, которые определяют порядок выполнения операций и влияют на результат вычислений, особенно в случае наличия знака «плюс» или «минус» перед числом.

1. Правило знака перед числом. Если перед числом стоит знак «плюс» или «минус», то этот знак определяет знак числа.

Примеры:

+5 — число 5 со знаком «плюс»

-3 — число 3 со знаком «минус»

2. Правило порядка операций. Порядок выполнения арифметических операций определяется следующими правилами:

а) Выполняются сначала операции в скобках;

б) Скобки могут быть вложенными, в этом случае сначала выполняются операции в самой внутренней паре скобок;

в) Затем выполняются умножение и деление слева направо;

г) В конце выполняются сложение и вычитание слева направо.

Примеры:

а) Выражение 2 + 3 * 4 будет равно 14, так как умножение выполняется перед сложением;

б) Выражение (2 + 3) * 4 будет равно 20, так как сначала выполняется операция в скобках;

в) Выражение 10 — 2 * 5 будет равно 0, так как умножение выполняется перед вычитанием.

Знание существующих правил позволяет проводить вычисления с точностью и избегать ошибок при решении арифметических задач.

Правило умножения и деления

При выполнении операций умножения и деления, существует определенный порядок выполнения. Этот порядок не зависит от наличия знаков плюс или минус перед операндами. Важно правильно интерпретировать данное правило, чтобы получить верный результат вычислений.

Правило умножения и деления можно запомнить, используя аббревиатуру «МДА» (множение, деление, а потом сложение и вычитание). Это означает, что сначала выполняются операции умножения и деления, а затем производятся операции сложения и вычитания.

Если в выражении, которое нужно вычислить, имеется несколько операций умножения или деления, их следует выполнять по порядку слева направо. Например, если дано выражение «5 * 2 / 10», сначала выполняется умножение «5 * 2», то есть получается результат «10». Затем этот результат делится на число «10», что даст итоговый результат «1».

Если в выражении присутствуют операции умножения или деления и сложения или вычитания, их необходимо выполнять последовательно согласно правилу «МДА». Например, в выражении «2 + 3 * 4», сначала производится умножение «3 * 4», что дает результат «12». Затем число «2» складывается с полученным результатом «12», и в итоге получается конечный результат «14».

Важно помнить, что операции в скобках всегда имеют высший приоритет, и их следует выполнять первыми. Если в выражении присутствуют скобки, необходимо выполнять операции внутри них до того, как перейти к другим операциям.

Правильное понимание и применение правила умножения и деления позволяет получать точные и верные результаты вычислений.

Правило сложения и вычитания

Правило сложения и вычитания в арифметике гласит, что операции сложения и вычитания выполняются в порядке, в котором они указаны в выражении.

Если в выражении присутствует как сложение, так и вычитание, то операции выполняются по очереди слева направо.

Например, в выражении «3 + 5 — 2» сначала выполнится сложение: 3 + 5 = 8, затем выполнится вычитание: 8 — 2 = 6.

Если в выражении имеется унарный знак плюс или минус перед числом, то такое число считается положительным или отрицательным соответственно.

Например, в выражении «+3 + (-5) — 2» сначала выполнится сложение: +3 + (-5) = -2, затем выполнится вычитание: -2 — 2 = -4.

Правило сложения и вычитания позволяет определить правильный порядок выполнения арифметических операций и получить корректный результат.

Видео:как ЛЕГКО сложить отрицательные числа , ПРИМЕРЫСкачать

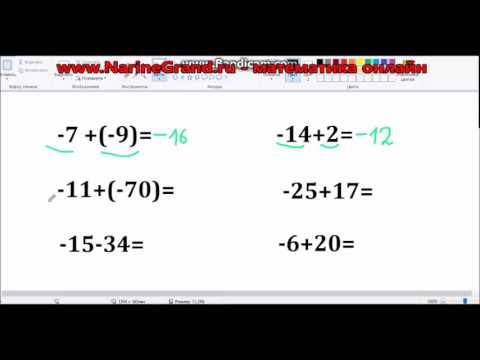
Знаки операций и их применение

Знак «+» используется для сложения чисел. Он позволяет нам объединять два или более числа в одну сумму. Например, 2 + 3 = 5. Приоритет операции получения суммы может быть изменен с использованием скобок.

Знак «-» может выполнять две основные функции: вычитание и обозначение отрицательного числа. Операция вычитания позволяет нам находить разницу между двумя числами. Например, 7 — 4 = 3. Знак минус также используется для обозначения отрицательного числа, которое находится слева от него. Например, -5.

Порядок операций в арифметике может быть определен при помощи скобок и приоритета определенных операций. Круглые скобки дают первостепенность операций внутри них. Это значит, что все, что находится внутри скобок, будет выполнено первым. Если в выражении есть несколько пар скобок, сначала вычисляются выражения, находящиеся внутри самых внутренних скобок.

Знаки операций впереди числа: плюс

В математике знак ‘+’, стоящий перед числом не является обязательным, так как положительность числа подразумевается по умолчанию. Однако в некоторых случаях использование знака ‘+’ может быть полезным.

Знак ‘+’ перед числом часто применяется для ясности и предотвращения возможных ошибок при чтении математических выражений. Он помогает отличать положительные числа от отрицательных, особенно в выражениях, содержащих как положительные, так и отрицательные числа.

Кроме того, знак ‘+’ может использоваться для передачи информации в программировании. Например, в некоторых языках программирования ‘+5’ может означать, что число 5 является положительным и обрабатывается соответствующим образом.

Однако следует отметить, что знак ‘+’ перед числом не влияет на само число. Он служит только для ясности и обозначения положительности.

Знаки операций впереди числа: минус

Когда перед числом ставится знак минус, это означает, что число отрицательное. Отрицательные числа можно использовать в арифметических операциях, а также в других математических выражениях.

Если перед числом стоит знак минус, то оно считается отрицательным и его значение будет меньше нуля. Например, число -5 означает, что мы имеем дело с отрицательным числом, которое меньше нуля на 5 единиц.

Знак минус может быть использован для вычитания чисел. Например, 10 — 5 означает, что мы берем число 10 и отнимаем от него число 5, результатом будет число 5.

Иногда использование знака минус впереди числа не обозначает отрицательность числа, а лишь указывает на отрицательное направление или ситуацию. Например, при описании координат в двумерном пространстве, если первое число отрицательное, это означает, что точка находится слева от начала координат.

Примеры использования знака минус:
-10
-3 — 2
-5 + 3

Знак минус впереди числа указывает на отрицательность числа и может использоваться в арифметических операциях и математических выражениях.

Видео:Сложение в разных системах счисления (2, 8, 16). Урок 5Скачать

Влияние знака операции на результат

Знак операции в арифметике имеет важное значение и может влиять на получаемый результат. В зависимости от знака операции (плюс или минус) решение выражения может быть положительным или отрицательным.

Если операция перед числом является плюсом (+), то результат будет положительным. Например, выражение «+5» равно 5.

Если операция перед числом является минусом (-), то результат будет отрицательным. Например, выражение «-5» равно -5.

Если операция унарная, то это означает, что она применяется только к одному числу. Например, в выражении «-(-5)» знак минуса перед числом применяется дважды и результатом является положительное число 5.

Порядок операций в арифметике также влияет на результат, поэтому важно обращать внимание на правила приоритета операций. Например, в выражении «-5 + 3» сначала выполняется унарная операция (-5), а затем сложение (-5 + 3), что дает результат -2.

Сложение и вычитание с разными знаками

Например, 5 + (-3). В этом случае мы вычитаем 3 из 5 по модулю и сохраняем знак числа 5, так как его модуль больше. Поэтому результатом будет 2. Аналогично, (-7) + 4 = (-3), так как мы вычитаем 4 из 7 по модулю и сохраняем знак числа 7.

Вычитание с разными знаками работает по аналогичному принципу. Если у нас есть выражение типа 8 — (-6), мы можем представить это как 8 + 6 и применить вышеизложенные правила сложения. В этом конкретном примере мы вычитаем 6 из 8 по модулю и сохраняем знак числа 8, получая результат 14.

Правила сложения и вычитания с разными знаками в арифметике помогают нам определить знаки результирующих чисел и выполнять арифметические операции с учетом этих знаков. Знание этих правил позволяет нам более точно проводить вычисления и избегать ошибок.

Умножение и деление с разными знаками

В арифметике существуют определенные правила для умножения и деления чисел с разными знаками.

Умножение двух чисел одного знака всегда будет положительным результатом. Например, умножение положительного числа на положительное или отрицательного числа на отрицательное всегда даст положительный результат. Например, 3 * 2 = 6 или (-3) * (-2) = 6.

Умножение двух чисел разных знаков всегда будет отрицательным результатом. Например, умножение положительного числа на отрицательное всегда даст отрицательный результат. Например, 3 * (-2) = -6.

Деление двух чисел с разными знаками всегда будет отрицательным результатом. Например, деление положительного числа на отрицательное всегда даст отрицательный результат. Например, 6 / (-2) = -3.

Исключение составляет деление нуля на любое число. Деление нуля на положительное или отрицательное число всегда будет равно нулю, так как ноль не имеет знака. Например, 0 / 2 = 0.

Таким образом, правила умножения и деления с разными знаками помогают определить знак конечного результата и сделать операции с числами более предсказуемыми.

Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать

Порядок операций и приоритеты

В математике существуют определенные правила, регулирующие порядок выполнения арифметических операций. Корректное применение этих правил позволяет избежать ошибок и получить верный результат.

Операции выполняются в следующем порядке:

Сначала выполняются операции в скобках.
Затем выполняются умножение и деление.
После этого выполняются сложение и вычитание.

Если в выражении присутствуют операции с одинаковым приоритетом, то они выполняются слева направо.

Например, рассмотрим выражение 5 + 3 * 2. В данном случае сперва выполняется умножение (3 * 2 = 6), а затем сложение (5 + 6 = 11). Если бы порядок операций был обратным, то результат был бы другим: (5 + 3) * 2 = 16.

Также стоит помнить о том, что операции в приоритете могут быть изменены с помощью использования скобок. Например, выражение (5 + 3) * 2 будет иметь результат 16, потому что сложение выполнится первым.

Итак, знание порядка операций и приоритетов является ключевым в арифметике и позволяет корректно выполнять сложные математические выражения, избегая ошибок.

Использование скобок

В арифметике существует порядок операций, который определяет, в какой последовательности выполняются различные арифметические операции. Однако, если требуется изменить этот порядок, можно использовать скобки. Скобки позволяют группировать операции и задавать им приоритет.

В арифметических выражениях с использованием скобок операции внутри скобок выполняются раньше, чем операции вне скобок. Таким образом, выражения внутри скобок имеют более высокий приоритет и вычисляются первыми.

Например, выражение (2 + 3) * 4 будет выполнено следующим образом:

1 шаг	`(2 + 3) * 4`	Вычисление выражения в скобках: `2 + 3 = 5`
2 шаг	`5 * 4`	Выполнение умножения: `5 * 4 = 20`

Без использования скобок выражение будет вычислено в соответствии с порядком операций. В примере выше без скобок выражение 2 + 3 * 4 будет выполнено следующим образом:

1 шаг	`3 * 4`	Выполнение умножения: `3 * 4 = 12`
2 шаг	`2 + 12`	Выполнение сложения: `2 + 12 = 14`

Таким образом, использование скобок позволяет точно определить порядок выполнения операций в арифметическом выражении, в том числе при использовании операций «+» и «-«.

Порядок операций в комплексных выражениях

При работе с комплексными выражениями важно соблюдать правильный порядок операций. Это позволяет получать верные результаты и избегать ошибок.

В общем случае, при вычислении комплексного выражения следует придерживаться следующего порядка операций:

Выполнение операций, находящихся внутри скобок.
Выполнение умножения и деления в порядке слева направо.
Выполнение сложения и вычитания в порядке слева направо.

Если в выражении имеется несколько операций одного уровня (например, несколько умножений), то они выполняются без изменения порядка. В таких случаях может быть полезно использование круглых скобок для явного указания порядка операций.

Также стоит обратить внимание на то, что комплексные выражения могут содержать различные математические функции, такие как синус, косинус и др. При вычислении комплексного выражения с функцией следует исполнять функцию в первую очередь, а затем выполнять остальные операции по обычному порядку.

Соблюдение правильного порядка операций позволит получать верные результаты при работе с комплексными выражениями и упростит процесс вычислений.

Видео:Арифметические действия в двоичной системе счисленияСкачать

Особые случаи и исключения

Хотя общий порядок операций в арифметике состоит в выполнении умножения и деления перед сложением и вычитанием, есть несколько особых случаев и исключений, которые стоит учитывать.

Если операторы плюс (+) или минус (-) используются как унарные операторы и стоят впереди числа или выражения, то они задают знак числа. Например:

+5 будет означать положительное число 5, а -5 будет означать отрицательное число 5.

Кроме того, важно помнить о приоритете операций внутри скобок. Если в выражении есть скобки, операции внутри скобок имеют самый высокий приоритет и выполняются первыми. Например:

Если у нас есть выражение 4 * (2 + 3), то сначала выполняется операция в скобках (2 + 3), которая дает результат 5, а затем производится умножение: 4 * 5, что дает итоговый результат 20.

Правильное понимание порядка операций и особых случаев позволяет избежать ошибок и получить точные результаты при выполнении арифметических вычислений.

Применение отрицательных чисел

Отрицательные числа применяются в различных сферах и ситуациях. Несколько примеров их использования:

Математика: в математических операциях отрицательные числа используются для обозначения отрицательной величины или направления. Они позволяют выполнять различные вычисления, включая сложение, вычитание, умножение и деление отрицательных чисел.
Температура: отрицательные числа используются для измерения низких температур. Отрицательные значения показывают отклонение температуры от нулевой отметки, например, при измерении температуры замерзания воды (0°С), значение ниже нуля градусов указывает на наличие мороза.
Финансы: отрицательные числа применяются в финансовой сфере для обозначения задолженности, убытков, потерь и расходов. Отображая отрицательное значение на финансовых отчетах, можно анализировать состояние предприятия или частного личного бюджета.
Координатная система: отрицательные числа используются для указания отрицательных направлений или положений на координатной плоскости. Они помогают определить точное местонахождение объекта в пространстве.
Статистика: отрицательные числа применяются в анализе данных и статистике для обозначения отрицательных величин, например, в случае долевой прибыли или убытка, обратных показателях роста или падения, и других отрицательных показателях, которые требуется учитывать при анализе.

Использование отрицательных чисел имеет широкий спектр применения и важно для точности и полноты описания различных явлений и процессов в различных областях науки, техники и повседневной жизни.